|
|
Munkatársak
| Oktatók |
Dr. Földi Péter
tanszékvezető
egyetemi docens, PhD
szoba: 234/A, tel: 54-4807
titan.physx.u-szeged.hu/~foldi/
|
|
Dr. Benedict Mihály
professor emeritus, az MTA doktora
szoba: 234/B, tel: 54-4369
www.staff.u-szeged.hu/~benedict/
|
|
Dr. Czirják Attila
tanszékvezető helyettes
tudomábyos munkatárs, PhD
szoba: 234/A, tel: 54-4807
www.staff.u-szeged.hu/~czirjak/
|
|
Dr. Fehér László
egyetemi tanár, az MTA doktora
szoba: 234/C, tel: 54-4811
www.staff.u-szeged.hu/~lfeher/
|
|
Dr. Gergely Árpád László
egyetemi tanár, az MTA doktora
félállásban
szoba: 232, tel: 54-4529
www.staff.u-szeged.hu/~gergely/
|
|
Dr. Gyémánt Iván
ny. egyetemi docens
a fizikai tudomány kandidátusa
szoba: 228, tel: 54-4282
www.staff.u-szeged.hu/~gyemant/
|
|
Dr. Iglói Ferenc
egyetemi tanár, az MTA doktora
félállásban
szoba: 228, tel: 54-4282
www.szfki.hu/~igloi/
|
|
Dr. Keresztes Zoltán
egyetemi docens, PhD
szoba: 229, tel: 54-4813
|
|
Dr. Papp György
ny. egyetemi docens, a fizikai tudomány kandidátusa
szoba: 229, tel: 54-4813
www.staff.u-szeged.hu/~pgy/
|
|
|
|
| Doktoranduszok,
predoktori ösztöndíjasok, demonstrátorok |
Fekecs Barna
PhD hallgató
barna.fekecs@gmail.com
|
|
Fóris Attila
demonstrátor
|
|
Gábor Bence
PhD hallgató
gabor.bence@stud.u-szeged.hu
szoba: 230
|
|
Nagy Cecília
PhD hallgató
szoba: 229
|
|
Gombkötő Ákos
predoktor
gombk.ak@gmail.com
|
|
Juhász Bence
PhD hallgató
bencebtgk@ gmail.com
szoba: 230, tel: 54-4663
|
|
Kasza József
PhD hallgató
Jozsef.Kasza@ eli-alps.hu
|
|
Magashegyi István
predoktor
szoba: 230, tel: 54-4663
|
|
Mike Péter
PhD hallgató
szoba: 230, tel: 54-4663
mikpet94@gmail.com
|
|
Pető Tamás
PhD hallgató
szoba: 230, tel: 54-4663
petotamas0@ gmail. com
|
|
Racskó Bence
PhD hallgató
szoba: 231, tel.: 54-4809
daeron806@ gmail. com
|
|
Sallai Krisztina
MSc hallgató, demonstrátor
krityo98@gmail.com
|
|
Szilasi Bálint Morgan
MSc hallgató, demonstrátor
szilasibm@ gmail. com
|
|
|
|
Korábbi munkatársak és vendégoktatók |
Dr. Bogár Ferenc
tud. főmunkatárs
c. egyetemi docens, PhD
tel: 54-4593
www.staff.u-szeged.hu/~bogar/
|
|
Dr. Dömötör Piroska
egyetemi adjunktus, PhD
titan.physx.u-szeged.hu/~dpiroska/
|
|
Dr. Görbe Tamás Ferenc
egyetemi adjunktus, PhD
https://tamasgorbe.com/
|
|
Dr. Hack Szabolcs
Hack.Szabolcs@physx. u-szeged. hu
|
|
Dr. Paragi Gábor
tud. főmunkatárs, PhD
tel: 54-4593
paragi@ sol. cc. u-szeged.hu
https://u-szeged.hu/ice/drug-development/biomimetic-systems/members
|
|
Dr. Varga Zsuzsanna
ny. egyetemi docens
|
|
Dr. Varró Sándor
MTA Wigner FK SZFI
tud. tanácsadó
egyetemi magántanár
az MTA doktora
www.szfki.hu/~vs/
|
|
|
|
| Adminisztratív
munkatársak |
Juhászné Miklós Melinda
ügyintéző
szoba: 227, tel: 54-4368
mmelinda @ titan.physx.u-szeged.hu
|
|
D'Angelo Róbert
hivatalsegéd
szoba: 227, tel: +36 62 544-121 (41-21)
d.angelo.robert @ med.u-szeged.hu
|
|
| Néhány
korábbi hallgatónk |
| Dr. Ayadi Viktor |
| Dr. Horváth Zsolt |
| Dr. Juhász Róbert |
| Dr. Karsai Márton |
| Dr. Kálmán Orsolya |
| Dr. Kovács Zoltán |
| Dr. Majorosi Szilárd |
| Dr. Mikóczi Balázs |
| Dr. Paragi
Gábor |
| Dr. Pusztai Béla Gábor |
| Dr. Roósz Gergő |
| Dr.
Serényi Tamás |
| Dr. Szabó Lóránt Zsolt |
| Dr. Szaszkó-Bogár Viktor |
Oktatás
Információk
Alapképzés (BSc)
Mesterképzés (MSc)
Doktori képzés (PhD)
Jegyzetek
- Benedict Mihály: Elektrodinamika, II. kiadás,
JATEPress, Szeged, 2000.
-
Benedict Mihály: Introduction to the physics of atoms molecules and photons, Szeged, 2013.
- Benedict Mihály:
Kvantummechanika
számítógépes animációkkal, Szeged, 2010.
- Benedict Mihály: Kvantumelektrodinamika és Kvantumoptika, Szeged, 2015.
- Benedict
Mihály: Quantum theory of atoms, molecules and their interaction with light, Szeged, 2013.
- Bogár Ferenc: Bevezető fejezetek a
molekulák elektronszerkezetének elméleti leírásába, Szeged, 2010.
- Gyémánt Iván: Fejezetek az analitikus
mechanikából, JATEPress, Szeged, 2007.
- Gyémánt Iván - Nagy Gál Katalin: Elméleti
mechanika ( Előadás jegyzetek),
JATEPress,
Szeged, 2008.
- Gyémánt Iván - Varga Zsuzsa: Matematikai
módszerek a fizikában, JATEPress, Szeged, 2009.
- Gyémánt Iván - Görbe Tamás Ferenc: Lineáris
algebra fizikusoknak, Polygon Jegyzettár, Szeged, 2011.
- Görbe Tamás Ferenc:
Lineáris algebra
fizikusoknak - Internetes melléklet, Szeged, 2011.
- Görbe Tamás Ferenc: Lineáris algebra
feladatgyűjtemény, Szeged, 2011.
- Hevesi Imre,
Gyémánt Iván: Félvezető optika, Szeged, 2013.
- Varró Sándor: Bevezetés az intenzív fény
és anyag kölcsönhatásainak elméleti leírásába, Szeged, 2010.
Demonstrátori pályázat (folyamatos)
Az Elméleti Fizikai Tanszék
szívesen veszi MSc hallgatók jelentkezését demonstrátori pozíció
betöltésére a tanszéken oktatott tárgyak gyakorlataihoz kapcsolódóan.
Érdeklődő hallgatók a tanszékvezetőnek küldött e-mailben vagy
személyesen jelentkezzenek!
Fehér László, tanszékvezető
Nyári szakmai gyakorlat az
Elméleti Fizikai Tanszéken (2018)
Aktuális témakiírások az Elméleti Fizikai Tanszéken
Attoszekundumos kvantumfizika (Czirják Attila)
Erős és rövid lézerimpulzusok és atomok kölcsönhatását felhasználva attoszekundumos fényimpulzusok állíthatóak
elő, amelyek új távlatokat nyitottak a fény-anyag kölcsönhatás vizsgálatában, pl. a szegedi ELI-ben is fog
üzemelni ilyen fényforrás. A gyakorlat célja megismerkedni a téma alapjaival, és elindítani a hallgató saját
elméleti vagy numerikus (TDK illetve szakdolgozati) kutatási témáját.
Előismeret: Jeles/jó jegyek
elméleti fizikából és matematikából.
Attoszekundumos fényimpulzus előállítása nemlineáris Thomson-szórással (Hack Szabolcs és Czirják Attila )
A nemlineáris Thomson-szórás a klasszikus elektrodinamika egyik legalapvetőbb jelensége, amikor relativisztikus
sebességre gyorsított elektron kölcsönhat erős lézertérrel. Ez a folyamat használható másodlagos sugárforrásként
attoszekundumos fényimpulzus előállítására. A gyakorlat célja megismerkedni a téma alapjaival, és elindítani a
hallgató saját elméleti vagy numerikus (TDK illetve szakdolgozati) kutatási témáját.
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
A fázistér geometriája és a hamiltoni redukció (Fehér László)
Egzaktul megoldható problémák a fizika sok területén fontosak és a matematika központi fejezeteihez is szorosan
kapcsolódnak. Ilyen „integrálható” rendszerek vizsgálatának egyik hatásos módszere a hamiltoni szimmetria
redukció. A hallgató megismerkedhet a módszer matematikai alapjaival, amelyet később kutatási problémák
megoldásához alkalmazhat.
Előismeret: Analitikus mechanika tárgy minimum jó szintű teljesítése, matematikai-fizikai affinitás,
szakszöveg olvasáshoz angol nyelvtudás.
Gravitációs hullámok (Gergely Árpád László és Keresztes Zoltán)
A gravitációs hullámokat az általános relativitáselmélet 100 éve jósolta meg, közvetlen kimutatásukat a LIGO
Tudományos Kollaboráció 2016-ban jelentette be, ebben a munkában a kutatócsoportunk is részt vett. Gravitációs
hullámok az erős gravitáció (erősen görbült téridő) tartományokból érkezhetnek hozzánk. Ilyenek az Ősrobbanás
előtti inflációs korszak, illetve az összeolvadó feketelyuk-párosok, melyek aktív galaxismagokban is előfordulnak,
és akkréciós folyamatokkal, energetikus jet-képződéssel is kapcsolatba hozhatók. A gravitációs hullámok analitikus
(egzakt és perturbatív), valamint numerikus módszerekkel tanulmányozhatók, illetve elektromágneses kísérő
jelenségek, valamint nagyenergiás kozmikus részecskék és neutrínó-kibocsátás jellemzik őket. A nyári gyakorlat
során a hallgatók az irodalom feldolgozása és számolási / programozási feladatok végrehajtásán keresztül
ismerkednek a területtel.
Előismeret: Angol nyelvtudás, számolási és programozási készség, szakmai alkalmasság megítélése személyes
elbeszélgetés / eddigi tanulmányi eredmények figyelembevételével.
Időfüggő nanoelektronikai problémák (Földi Péter)
Az utóbbi időkben a kísérleti technológia fejlődése lehetővé tette szilárdtest rendszerekben a töltéshordozók PHz
sebességű kontrollját. A gyakorlat folyamán betekintést nyerhetünk ezeknek az ultragyors folyamatoknak a
dinamikájába, miközben a transzportfolyamatok leírásának alapjaival is megismerkedünk. Fő célunk a
lézerimpulzussal létrehozott áramok kvantummechanikai leírása. Az elsajátított módszerek szilárdtest rendszerek
mellett általánosabb szóráselméleti problémák kezelésére is alkalmasak.
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
A bolyongás problémája és egyszerű fizikai alkalmazásai (Iglói Ferenc)
A bolyongással kapcsolatos legegyszerűbb
eredmények áttekintése után azok általánosításait és egyszerű fizikai
alkalmazásait kell áttanulmányozni.
Előismeret: Nincs.
Szakdolgozati (BSc)
témakiírások az Elméleti Fizikai Tanszéken (2017)
Aktuális témakiírások az
Elméleti Fizikai Tanszéken
Kölcsönható
töltésrendszer mozgásegyenlete a késleltetés figyelembe vételével
(Benedict Mihály)
Mozgó töltések rendszere nem konzervatív, a
mágneses erő sebességfüggő, és a mozgó töltés által keltett mező is
változik. A mozgás Newton-féle leírása helyett ilyen bonyolult esetben
a Lagrange-Hamilton formalizmus alkalmazása vezethet eredményre. A
feladat a megfelelő mozgásegyenletek tanulmányozása.
Irodalom: Landau-Lifsic:
Elméleti Fizika II, Jackson: Klasszikus Elektrodinamika
Előismeret: Elméleti mechanika,
Elektrodinamika, Angol nyelvismeret szükséges
A
fény pályaimpulzusnyomatékának klasszikus elektrodinamikai tárgyalása
(Benedict Mihály)
A Maxwell egyenletek jól ismert síkhullám
megoldásán túl számos további megoldása van, amelyek sajátossága, hogy
a polarizációs tulajdonságaik által meghatározott perdületen túlmenően
is szállíthatnak kvantált impulzusnyomatékot. A feladat ezeknek a
hullámformáknak a tanulmányozása.
Előismeret: Elméleti mechanika,
Elektrodinamika, Angol nyelvismeret szükséges
A
Toda molekula: egy nevezetes klasszikus integrálható rendszer (Fehér
László)
Egzaktul megoldható sokrészecske rendszerek talán
legtöbbet kutatott osztályát alkotják a Toda rendszerek, amelyek egy
dimenzióban mozgó, exponenciális függvénnyel adott potenciállal
kölcsönható tömegpontokat írnak le. Bár az ezek között is legegyszerűbb
"Toda molekula" tanulmányozása kb. 40 éve folyik, a téma manapság is
érdekes matematikai-fizikai kérdések forrása. A hallgató feladata a
Toda rendszerekkel és általánosításaikkal kapcsolatos ismeretek
elsajátítása és áttekintése után a nyitott kérdések tisztán elméleti,
analitikus vizsgálata, amelyre még intenzívebb módon később TDK illetve
MSc dolgozat készítése is lehetőséget nyújthat.
Előismeret: Matematikai készség
és érdeklődés, "analitikus mechanika" tárgy előzetes teljesítése
minimum négyes érdemjeggyel, angol nyelvtudás irodalmazáshoz
Vállalt hallgatói létszám: 1
hallgató
Időfüggő
kvantummechanikai problémák (Földi Péter)
Külső terek hatására egy kvantumrendszer
dinamikáját meghatározó Hamilton-operátor gyakran explicit időfüggéssel
rendelkezik. A tervezett munka ilyen rendszerek időfejlődésének a
megismerésére irányul, párhuzamosan alkalmazott, egymást kiegészítő
analitikus és numerikus módszerekkel. Az eszközkészlet elsajátítása és
az alapvető modellek megismerése jó kiindulópontot szolgáltat lézerrel
kölcsönható atomi, molekuláris vagy nanoméretű rendszerek
vizsgálatához, de szilárdtestfizikai transzportproblémák megoldásához
is.
Előismeret: Jeles/jó jegyek
elméleti fizikából és matematikából
Gravitációs
szabadsági fokok a skalár-tenzor elméletekben (Gergely Árpád László)
Az általános relativitáselméletet általánosító
legegyszerűbb gravitációs elméletek a metrikus tenzor mellett egy
skalármezőt is tartalmaznak. Amennyiben a skalármező dinamikájára
egyszerű egyenlet vonatkozik (Jordan frame) a metrikára az
Einstein-egyenletnél bonyolultabb egyenlet adódik. Konformis átskálázás
után lehetséges azonban olyan metrikát találni, melyre az Einstein
egyenlet vonatkozik (Einstein frame), ebben az esetben viszont a
skalármező dinamikája bonyolultabb. A szakirodalomban elterjedt
állítás, hogy a kétféle leírás ekvivalens fizikához vezet, nevezetesen
a gravitációs szabadsági fokok azonosak. A szakdolgozat célja a kétféle
leírásban adódó gravitációs hullámok összehasonlítása, különös
tekintettel a skalár-tenzor elméletekben fellépő ötféle polarizációra.
Előismeret: Elemi
differenciálgeometria, általános relativitáselmélet, és angol nyelv
A
bolyongás problémája és egyszerű fizikai alkalmazásai (Iglói Ferenc)
A bolyongással kapcsolatos legegyszerübb
eredmények áttekintése után azok általánosításait és egyszerű fizikai
alkalmazásait kell áttanulmányozni.
Spin-dominált
hullámforma fáziskorrekcióinak vizsgálata (Gergely Árpád László és
Keresztes Zoltán)
A spin-dominált hullámformák a jelentősen eltérő
tömegekkel rendelkező fekete lyuk kettősök által kisugárzott
gravitációs hullámokat modellezik. A szakdolgozat célja e hullámformák
2.5, 3, 3.5 poszt-newtoni rendű fáziskorrekcióinak a meglévő (fázisban
2 poszt-newtoni rendig pontos) hullámforma kódba történő implementálása
és a korrekcióknak a hullámformákra gyakorolt hatásainak tanulmányozása.
Előismeret:
Differenciálgeometriai és általános relativitáselméleti alapok, angol
nyelv ismeret
Hallgatói szemináriumok
Aktuális szeminárium
2019. április 24. (szerda) 16:00, Lánczos Kornél tanterem
Előadó: Keresztes Zoltán (SZTE Elméleti Fizikai Tanszék)
Cím: Sajátperdülettel rendelkező test időfejlődése az általános relativitáselméletben
Kivonat |
Poszter |
Jegyzet
A pontszerű tömeges próbatest geodetikus pályát követ görbült téridőben.
A kiterjedt forgó test pályája azonban eltér a geodetikustól, ha a téridő
görbület, illetve a spin nagysága számottevő. A szemináriumon először a
speciális relativitáselméletben származtatjuk a spinnel rendlekező test
mozgását meghatározó egyenletrendszert, majd pedig az általános relativitáselméletben,
eljutva a Mathisson--Papapetrou--Dixon-egyenletekhez. Áttekintjük a származtatáshoz
szükséges matematikai eszközöket. A Mathisson--Papapetrou--Dixon-egyenletek a
test reprezentatív pontját meghatározó spin mellékfeltétellel záródnak.
A spinvektort a Frenkel--Mathisson--Pirani spin mellékfeltétel esetén vezetjük be,
majd származtatjuk annak fejlődés egyenletét a test sajátrendszerében.
Köszönetnyilvánítás: Az Emberi Erőforrások Minisztériuma UNKP-18-4 kódszámú Új Nemzeti Kiválóság programjának
támogatásával készült.
Korábbi szemináriumok
Diplomamunka (MSc)
témakiírások az Elméleti Fizikai Tanszéken (2017)
Aktuális témakiírások az
Elméleti Fizikai Tanszéken
Kölcsönható
töltésrendszer mozgásegyenlete a késleltetés figyelembe vételével
(Benedict Mihály)
Mozgó töltések rendszere nem konzervatív, a
mágneses erő sebességfüggő, és a mozgó töltés által keltett mező is
változik. A mozgás Newton-féle leírása helyett ilyen bonyolult esetben
a Lagrange-Hamilton formalizmus alkalmazása vezethet eredményre. A
feladat a megfelelő mozgásegyenletek tanulmányozása.
Irodalom: Landau-Lifsic:
Elméleti Fizika II, Jackson: Klasszikus Elektrodinamika
Előismeret: Elméleti mechanika,
Elektrodinamika, angol nyelvismeret szükséges.
A
fény pályaimpulzusnyomatékának klasszikus elektrodinamikai tárgyalása
(Benedict Mihály)
A Maxwell egyenletek jól ismert síkhullám
megoldásán túl számos további megoldása van, amelyek sajátossága, hogy
a polarizációs tulajdonságaik által meghatározott perdületen túlmenően
is szállíthatnak kvantált impulzusnyomatékot. A feladat ezeknek a
hullámformáknak a tanulmányozása.
Előismeret: Elméleti mechanika,
Elektrodinamika, angol nyelvismeret szükséges.
Relativisztikus
integrálható sokrészecske-rendszerek (Fehér László)
1986-ban Ruijsenaars és Schneider felfedezték,
hogy bizonyos relativisztikusan invariáns mezőegyenletek (pl. az ún.
sine-Gordon egyenlet) részecskeszerű, szoliton megoldásait véges
szabadsági fokú klasszikus és kvantummechanikai rendszerekkel lehet
modellezni. Ezek a modellek tetszőleges részecskeszám esetén egzaktul
megoldhatóak. A diplomamunka célja a háttérismeretek elsajátítása után
a Ruijsenaars-Schneider modellek olyan aktuális kérdéseinek vizsgálata,
amelyek csoportelméleti és analitikus mechanikai módszerekkel
tárgyalhatóak.
Előismeret: "Analitikus
mechanika" és "Szimmetriák a fizikában" tárgyak minimum jó szintű
teljesítése, matematikai-fizikai affinitás, angol nyelvtudás.
Időfüggő kvantummechanikai problémák (Földi Péter)
Külső terek hatására egy kvantumrendszer
dinamikáját meghatározó Hamilton-operátor gyakran explicit időfüggéssel
rendelkezik. A tervezett munka ilyen rendszerek időfejlődésének a
megismerésére irányul, párhuzamosan alkalmazott, egymást kiegészítő
analitikus és numerikus módszerekkel. Az eszközkészlet elsajátítása és
az alapvető modellek megismerése jó kiindulópontot szolgáltat lézerrel
kölcsönható atomi, molekuláris vagy nanoméretű rendszerek
vizsgálatához, de szilárdtestfizikai transzportproblémák megoldásához is.
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
Ultrarövid lézerimpulzusok terében mozgó töltött részecskék (Földi
Péter)
Az utóbbi években nagy érdeklődést váltott ki az a lehetőség, hogy intenzív lézerek tere részecskegyorsításra is
felhasználható.
Bár így a hagyományos részecskegyorsítóknál lényegesen kompaktabb eszközökkel lehetne nagyenergiás
részecskenyalábot létrehozni,
magának a nyalábnak a tulajdonságai egyelőre még elmaradnak a hagyományos gyorsítókban produkálható
paraméterektől.
A diplomamunka során a lézertérben mozgó töltött részecskék elméleti leírását lehet elsajátítani,
továbbá konkrét kísérleti elrendezések elemzése a feladat.
A téma összhangban van az EFOP-3.6.2-16-2017-00005 projekt kutatási céljaival
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
Fény-anyag kölcsönhatás a femtoszekundumos időskálán: félklasszikus és
teljesen kvantumos leírás (Földi Péter)
Napjainkban egyre gyakoribbak azok a lézerrendszerek, amelyek ultrarövid,
femtoszekundumos időtartamú elektromágneses impulzusokat képesek szolgáltatni.
Így vizsgálhatóvá, sőt esetlegesen kontrollálhatóvá váltak hasonló időskálán
lezajló atomi-molekuláris vagy szilárdtestekben lezajló folyamtok.
A fény-anyag kölcsönhatás elméleti leírása szempontjából ez az időskála,
illetve az ide kapcsolódó kevés ciklusú lézerimpulzusok hatása túlmutat
a problémakör hagyományos tárgyalásán. A diplomaunka témája a fent
leírt lézerimpulzusok és anyagi rendszerek kölcsönhatásának vizsgálata,
jellemzően időtartományban.
A téma összhangban van az EFOP-3.6.2-16-2017-00005 projekt kutatási céljaival
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
Analitikus és numerikus számítások ultrarövid fényimpulzusokkal gerjesztett
atomi és szilárdtest rendszerek modellezésére (Földi Péter)
Ultrarövid fényimpulzusok anyaggal való kölcsönhatásának elméletében az alapvető
egyenletek jól ismertek, ugyanakkor megoldásuk gyakran komoly numerikus
számításokat igényel. A diplomamunka készítése során először lehetőség adódik
az elméleti alapok megismerésére, majd a szükséges numerikus készségek is elsajátíthatók.
A számítógéppel kapott eredményeket ezután összevetjük a nem nagy számban létező,
így a területen kiemelkedően fontos analitikusan megoldható modell jóslataival,
és maghatározzuk e modellek alkalmazhatóságának határait.
A téma összhangban van az EFOP-3.6.2-16-2017-00005 projekt kutatási céljaival
Előismeret: Jeles/jó jegyek elméleti fizikából és matematikából.
Fekete
lyukak vizualizációjával kapcsolatos jelenségek a skalár-tenzor
elméletekben (Gergely Árpád László)
A fekete lyukak bár definíció szerint
láthatatlanok, jelentős hatással vannak elektromágneses sugárzást
kibocsájtó környezetükre. A hatás megnyilvánulhat a fénypályák
elhajlásában (gravitációs lencsézés), a körülötte keringő plazmakorong
sugárzásában és az általa keltett mágneses tér kialakításában, mely
nagyenergiás részecskékből álló jet kialakulásához vezet. Ezen
folyamatok látványos szemléltetését láthattuk nemrég az Interstellar
filmben, de ezeket komoly szakcikkek is ismertetik. A diplomamunka
célja a jelenségkör megértése, majd kiterjesztése az Einstein
gravitációelméletét általánosító legegyszerűbb gravitációs elméletekben
megjelenő fekete lyukakra.
Előismeret: Bevezetés az
általános relativitáselméletbe előadás jó vagy jeles elvégzése, angol
nyelvtudás.
Határátmenetek
tulajdonságai elektromágneses és gravitációs terekben, plazmákban
(Gergely Árpád László)
Különböző közegeket elválasztó határfelületeken
való áthaladáskor az elektromágneses és gravitációs térmennyiségek
egyik része folytonosan változik, másik része ugrást szenved el,
melynek nagyságát a felületi forrás határozza meg. Hasonló jelenségek
következnek be plazmában is, ha két plazmaréteg áramlási sebessége
különböző. Utóbbi esetben ismert jelenség a Kelvin-Helmholtz
instabilitás, mely látványos atmoszférikus jelenségekhez is vezet. A
diplomammunka célja az említett jelenségek rendszerezése majd a
Kelvin-Helmholtz instabilitás analógiáinak keresése gravitációs
rendszerekben (például lökéshullámok által elválasztott kozmikus
tartományokban).
Előismeret: Elektrodinamika és
Bevezetés az általános relativitáselméletbe előadások jó vagy jeles
elvégzése, angol nyelvtudás.
Sötét
anyag modellek vizsgálata galaktikus forgásgörbék és diszperziós
sebességek segítségével (Gergely Árpád László és Keresztes Zoltán)
A galaxisokat nagyméretű, a barionikus
komponensnél átlagban tízszer nagyobb tömegű, láthatatlan sötét anyag
halo dominálja. Ennek tanulmányozása a látszó komponensek keringési
sebességének és a sebesség diszperziójának vizsgálatán keresztül
lehetséges. A diplomamunka célja a módszerek elsajátítása, az általános
sebességdiszperziós modellek analitikus és numerikus vizsgálata,
valamint konkrét sötét anyag modellek tesztelése.
Előismeret: Bevezetés az
általános relativitáselméletbe előadás jó vagy jeles elvégzése, angol
nyelvtudás, programozási készség (Maple, C, Gnuplot).
Rendezetlen
kvantum spinláncok renormálása (Iglói Ferenc)
Kvantum rendszerek alapállapotában T=0
hőmérsékleten bekövetkező fázisátalakulások erősen befolyásolják ezen
rendszerek alacsonyhőmérsékletű termodinamikai viselkedését. A mintába
befagyott rendezetlenség jelenlétében vizsgáljuk ezen fázisátalakulás
tulajdonságait. Az egyszerűség kedvéért egydimenzióban dolgozunk és a
renormálási csoport módszer különböző variánsait használjuk. Analitikus
számolásokat és numerikus, számítógépes vizsgálatokat is végzünk.
Előismeret: Kvantummechanika és
statisztikus fizika jeles/jó jegyekkel, angol nyelvtudás az
irodalmazáshoz.
Spines
részecske mozgása forgó fekete lyuk téridőben (Keresztes Zoltán)
A kompakt kettős rendszerek mozgásának tárgyalása
több évtizedre tekint vissza. Ennek ellenére egészen napjainkig
fedeznek fel új típusú pályamozgásokat. Igen érdekes példák erre azok a
nagy excentricitású pályák, amelyeken a pericentrum közelében a sokkal
kisebb tömegű próbatest igen közel kerül a központi nagytömegű
objektumhoz. A pericentrum elfordulás pedig olyan sebes, hogy annak
környezetében tartózkodva a próbatest többször körbejárja a nagyobb
tömegűt, amíg újra megtudja közelíteni az apocentrumot. Ennek
eredményeképpen több levelű lóhereszerű pályák rajzolódnak ki. E
ráközelítő-pörgő ("zoom-whirl") pályákat 2002-ben fedezték fel abban a
határesetben, amikor a próbatest sajátperdülete (spinje) elhanyagolható
a másikéhoz képest (próbarészecske geodetikus mozgása Kerr-téridőben).
A diplomamunka céljai: i) megállapítani, hogyan módosítja a
próbarészecske spinje a ráközelítő-pörgő pályákat, ii) a spin irányának
numerikus fejlesztése a Mathisson–Papapetrou–Dixon-egyenletek alapján.
Előismeret: Bevezetés az
általános relativitáselméletbe előadás jó vagy jeles elvégzése, angol
nyelvtudás.
Az EFOP-3.6.2-16-2017-00005 projekthez kapcsolódó témák
Fizikus Teaház -
Bemutatkozik az Elméleti Fizikai Tanszék
- Mikor? 2015. április 1. (szerda) 18:00
- Hol? Bay Zoltán Tanterem (BO-202-3)
Tervezett program (~10-15
perces előadások)
- Gyémánt Iván: Lánczos Kornél élete
[Előadás]
- Czirják Attila: Atomok és fény
kölcsönhatása femto- és attoszekundumos időskálán [Előadás]
- Roósz Gergő: Rendeződés és dinamika
soktest rendszerekben [Előadás]
- Gergely Árpád László, Keresztes Zoltán: Gravitáció
és kozmológia [Előadás]
- Fehér László: Szimmetriák és
integrálhatóság [Előadás]
- Papp György: Alacsony dimenziós
elektronok
Beharangozó
Rendezvényünk fő célja az Elméleti Fizikai
Tanszéken folyó kutatások bemutatása, amellyel informálni szeretnénk a
Nyári szakmai gyakorlat, Projektmunka, TDK, Szakdolgozat vagy
Diplomamunka lehetőségek iránt érdeklődő hallgatóinkat:
- Mit és hogyan csinál a fizikus, különös
tekintettel az elméleti fizikus?
- Hallgatóként milyen munkához lehet csatlakozni?
- Milyen előismeretek, készségek és képességek
szükségesek ehhez?
Közvetlen, kötetlen hangú rendezvényünkre minden érdeklődőt szeretettel
várunk!
Kutatás
Tanszékünk munkatársainak
főbb kutatási területei
|
Integrálható rendszerek (Fehér László és munkatársai) |
Egzaktul megoldható ("integrálható") modellek fontos szerepet játszanak
a fizika szinte minden ágában. A megoldhatóság hátterében általában
valamilyen szimmetria áll, amely az integrálható
rendszerek extrém matematikai szépségét is garantálja. Fehér
László kutatásai hosszú idő óta erre a területre esnek, Kepler-szerű
rendszerektől kezdve konform térelméleti modelleken és szimmetria
algebráikon át szoliton egyenletek és klasszikus dinamikai Yang-Baxter
struktúrák vizsgálatáig. Az utóbbi évek kiemelt témája Calogero-Moser-Sutherland
és Ruijsenaars-Schneider
típusú egydimenziós sokrészecske rendszerek leírása. Ezek a modellek a
fizika számos területén megjelennek és sok szálon kapcsolódnak a
matematika érdekes fejezeteihez. A kutatás fő célja a modellek és
dualitási relációik egységes csoportelméleti értelmezésének
kidolgozása, elsősorban hamiltoni redukciós módszerek alkalmazásával. |
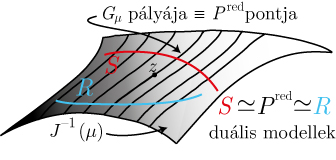
A hamiltoni redukció és Ruijsenaars
dualitás geometriája
|
|
Válogatott
publikációk
- B. Cordani, L. Fehér and P.A. Horváthy, Kepler-type
dynamical symmetries of long-range monopole interactions, J.
Math. Phys. 31, 202-211 (1990). [PDF]
- J. Balog, L. Fehér, L. O'Raifeartaigh, P.
Forgács and A. Wipf, Toda theory and W-algebra from a gauged
WZNW point of view, Ann. Phys. (N. Y.) 203, 76-136 (1990). [PDF]
- L. Fehér, L. O'Raifeartaigh, P. Ruelle,
I. Tsutsui and A. Wipf, On Hamiltonian reductions of the
Wess-Zumino-Novikov-Witten theories, Phys. Rep. 222, 1-64
(1992). [PDF]
- L. Fehér, J. Harnad and I. Marshall, Generalized
Drinfeld-Sokolov reductions and KdV type hierarchies,
Commun. Math. Phys. 154, 181-214 (1993). arXiv:hep-th/9210037
- J. de Boer and L. Fehér, Wakimoto
realizations of current algebras: an explicit construction,
Commun. Math. Phys. 189, 759-793 (1997). arXiv:hep-th/9611083
- J. Balog, L. Fehér and L. Palla, Chiral
extensions of the WZNW phase space, Poisson-Lie symmetries and groupoids,
Nucl. Phys. B 568, 503-542 (2000). arXiv:hep-th/9910046
- L. Fehér, I. Tsutsui and T. Fülöp, Inequivalent
quantizations of the three-particle Calogero model constructed by
separation of variables, Nucl. Phys. B 715, 713-757 (2005). arXiv:math-ph/0412095
- L. Fehér and B.G. Pusztai, A
class of Calogero type reductions of free motion on a simple Lie group,
Lett. Math. Phys. 79, 263-277 (2007). arXiv:math-ph/0609085
- L. Fehér and C. Klimcik, Self-duality
of the compactified Ruijsenaars-Schneider system from quasi-Hamiltonian
reduction, Nucl. Phys. B 860, 464-515 (2012). arXiv:1101.1759
[math-ph]
-
L. Fehér and I. Marshall,
Global description of action-angle duality for a Poisson-Lie deformation of the trigonometric
$BC_n$
Sutherland system
, Ann. Henri Poincaré 20, 1217-1262 (2019).
arXiv:1710.08760 [math-ph]
-
L. Fehér,
Poisson-Lie analogues of spin Sutherland models
, Nucl. Phys. B 949, 114807 (2019).
arXiv:1710.08760 [math-ph]
-
L. Fehér,
Bi-Hamiltonian structure of Sutherland models coupled to two u(n)*-valued spins from Poisson reduction
, Nonlinearity 35, 2971–3003 (2022).
arXiv:2109.07391 [math-ph]
|
Az alább látható listán a tanszék munkatársai
által az utóbbi 10 évben publikált tudományos közleményeket gyűjtőttük
össze. A lista a Magyar
Tudományos Művek Tára adatbázis alapján készült, ahol
korábban publikált cikkek és kutatók egyéni publikációs listái is
megtalálhatók.

Szeminárium
Aktuális szeminárium
2023. október 19. (csütörtök) 13:00
Előadó: Varró Sándor
Cím: Neumann János egyértelműségi tétele és holomorf függvények Hilbert-terei a kvantumoptikában.
Kivonat |
Előadás
Neumann János a Schrödinger-féle hely- és impulzusoperátorok (illetve ezek Weyl-féle alakjának)
egyértelműségét diszkrét paraméterű koherens állapotok segítségével bizonyította [1]. Vehetjük úgy is,
hogy a Bargmann által később bevezetett [2] holomorf függvénytér egy speciális bázisát alkotta meg
(amelynek teljességét később bizonyították). Az előadás első részében röviden bemutatjuk a teljes
komplex síkon értelmezett holomorf függvények terét [2], illetve a Neumann-rácsállapotokat [1],
amelyek jól használhatók bizonyos speciális prolémák megoldásához [3], [4].
A második részben közlendő eredményeket a korábban bevezetett reguláris fázisállapotok [5]
tulajdonságaiból vezetjük le. Ezek a speciális SU(1,1) koherens állapotok egyrészt egy új F
exponenciális fázisoperátor [5] sajátállapotai, a komplex egységkörlap belsejéhez tartozó z
sajátértékekkel. Másrészt olyan U(g) unitér operátorokkal állíthatók elő a vákuumból, amelyek egy
parametrikus kölcsönhatás evolúciós operátorátorai, ahol g a forrást jellemző komplex z paramétert és
az eltelt időt tartalmazza. Bebizonyítjuk, hogy a vizsgált rendszer Hamilton dinamikájának
tranzitivitása akkor biztosított, ha a megfelelő {g} paraméterhalmaz kielégíti a komplex
egységkörlapon értelmezett Möbius-transzformációk számolási szabályait. Ez egyben azt is jelenti,
hogy a kvantum fázistér mozgásai a Bolyai-Lobacsevszkíj síkon értelmezhetők. Azt is megmutatjuk,
hogy az új F exponenciális fázisoperátor [5] U(g) által generált transzformációja F tört-lineáris, azaz
(operátor-) Möbius-függvényét eredményezi, tehát F ún. “homogén kontrakció” [6]. Végül
bebizonyítjuk, hogy ha a Hilbert tér elemeit a reguláris fázisállapotokra vetítjük, akkor z holomorf
függvényeit kapjuk az egységkör belsejében, amelyek ún. súlyozott Bergman-teret [7] alkotnak.
Irodalom.
[1] Neumann J v 1931 Die Eindeutigkeit der Schrödingeschen Operatoren. Mathematische Annalen 104, 415-458 (1931).
[2] Bargmann, V 1961 On a Hilbert space of analytic functions and an associated integral transform. Commun. Pure and Applied Math., 14, 187-214 (1961).
[3] Schweber S 1967 On the application of Bargmann Hilbert spaces to dynamical problems. Annals of Physics 41, 205-229 (1967).
[4] Gombkötő Á, Varró S, Mati P, and Földi P 2020 High-harmonic generation as induced by a quantized field: Phase-space picture. Physical Review A 101, 013418 (2020).
[5] Varró S 2015 Regular phase operator and SU(1,1) coherent states of the harmonic oscillator. Physica Scripta 90, 074053 (2015).
[6] Kérchy L 1999 On homogeneous contractions. Journal of Operator Theory 41, 121–126 (1999).
[7] Hedenmalm H, Korenblum B and Zhu K, Theory of Bergman spaces. (Springer Graduate Texts in Mathematics 199 (2000)).
Korábbi szemináriumok
2023. október 5. (csütörtök) 13:30
Előadó: Kiss Tamás
Cím: A kvantumkommunikáció jelene és jövője
Kivonat |
Előadás
2023. október 5. (csütörtök) 13:00
Előadó: Ádám Péter
Cím: Multiplexelt egyfotonforrások
Kivonat |
Előadás
2023. április 27. (csütörtök) 13:00
Előadó: Trényi Róbert (University of the Basque Country, Wigner FK)
Cím: Metrológiailag hasznos valódi soktest-összefonódás aktiválása
Kivonat |
Előadás
Kvantum metrológiában a cél egy kvantumrendszer Hamilton-operátorába
kódolt paraméterek minél pontosabb becslése. Egy kvantumállapot
metrológiai hasznossága úgy jellemezhető, hogy mennyivel pontosabb
paraméterbecslést tesz lehetővé, mint bármely szeparálható állapot.
Ismert, hogy a maximális hasznosság elérésének szükséges feltétele,
hogy a metrológiára használt állapot valódi soktest-összefonódott legyen.
Viszont léteznek olyan valódi soktest-összefonódott állapotok amelyek nem
hasznosak metrológiailag, azaz nem teljesítenek jobban paraméterbecslés
szempontjából a szeparálható állapotoknál. Az előadásban azt vizsgáljuk
meg, hogy adott állapotok metrológiai hasznossága javítható-e, ha az
állapot több példányát vesszük. Megadunk összefonódott állapotok egy
olyan osztályát, amelyben minden állapotra igaz, hogy kellően sok példányt
véve elérhető velük a maximális metrológiai hasznosság. Érdekes módon ez
az osztály tartalmaz olyan állapotokat is, amik egy példányban nem hasznosak
metrológiára. Tehát kellően sok példánnyal az állapot metrológiailag hasznos
valódi soktest-összefonódottságát aktiválhatjuk. Megmutatjuk, hogy a sémánkkal
a fenti osztály állapotai a példányok számának növelésével exponenciális
gyorsasággal érik el a maximális hasznosságot. Továbbá, megvizsgáljuk a sémánk
hatékonyságát a fent említett osztályon kívüli állapotokra is.
2022. október 13. (csütörtök) 13:00
Előadó: Varró Sándor (Wigner FK SZFI, ELI-ALPS)
Cím: Préselt fotonszám-sajátállapotok és préselt hősugárzás
Kivonat |
Előadás
A kvantummechanikai harmonikus oszcillátor koherens [1] és préselt
(„squeezed”) állapotait [2] már Schrödinger (1926) és Kennard (1927)
meghatározták, közvetlenül a hullámmechanika megszületése után. Ezek
az állapotok a múlt század hatvanas éveitől a kvantumoptikában és
informatikában is fontos szerepet játszanak pl. a lézerek és
parametrikus folyamatok elméleti és kísérleti vizsgálatában [3], [4].
A préselt (koherens) állapotok az intenzív kvantált elektromágneses
sugárzás és elektronok kölcsönhatásának nem-perturbatív leírásában is
természetes módon megjelennek (pl. a magasrendű felharmonikusok
keltésének vizsgálatakor [5]), s így az attoszekundumos fizikában is
jelentőséggel bírnak.
A préselt (általános) koherens állapotok fotonszám-eloszlása jól
ismert [3], mondhatnánk tankönyvi anyag. A valószínűségi amplitúdókat
a préselés S (Bogoljubov-transzformáció) és az eltolás D operátora
szorzatának típusú mátrixelemei határozzák meg, amelyek
klasszikus Hermite- ill. Laguerre-polinomok egyszerű kifejezései.
Ugyanakkor az elmúlt több mint kilencven év igen kiterjedt irodalmában
a préselt szám-sajátállapotokra vonatkozó ( típusú, teháta D
eltolást nem tartalmazó) mátrixelemekre nem publikáltak hasonlóan
kompakt kifejezést.
Nemrég megmutattuk [6], hogy a préselt fotonszám-sajátállapotok
valószínűségi amplitúdói egyszerű zárt alakban kifejezhetők
klasszikus Gegenbauer-polinomokkal. Az előadásban, ennek az
eredménynek egyik alkalmazásaként, elemezzük a koherens és fekete
sugárzásban lejátszódó parametrikus emissziós és abszorbciós
folyamatokat [6]. Kitérünk arra is, hogy a [6] referenciában használt
módszerrel a préselt hősugárzás sűrűségmátrixa is meghatározható.
[1] Schrödinger E, Der stetige Übergang von der Mikro- zur
Makromechanik. Die Naturwissenschaften 14, 664-666 (1926).
[2] Kennard E H, Zur Quantenmechanik einfacher Bewegungstypen. Z.
Physik 44, 326-352 (1927).
[3] Dodonov V V, Nonclassical states in quantum optics: a squeezed
review of the first 75 years.J. Opt. B: Quantum Semiclass. Opt.
4,**R1–R33 (2002).
[4] Andersen U L, Gehring T, Marquardt C and Leuchs G 2016, 30 years
of squeezed light generation. Phys. Scr. 91, 053001 (2016).
[5] Varró S, Quantum optical aspects of high-harmonic generation.
Photonics 2021, 8, 269 (2021).
[https://doi.org/10.3390/photonics8070269].
[6] Varró S, Coherent and incoherent superposition of transition
matrix elements of the squeezing operator. New Journal of Physics 24,
053035 (2022). [https://doi.org/10.1088/1367-2630/ac6b4d].
2022. szeptember 15. (csütörtök) 12:30 (Riesz terem)
(közös szeminárium a Geometria Tanszékkel)
Előadó: Racskó Bence (SZTE, Elméleti Fizikai Tanszék)
Cím: A variációszámítás inverz problémája
Kivonat |
Előadás
A variációszámítás inverz problémájának célkitűzése
meghatározni, hogy melyek azok a differenciálegyenletek, amelyek
variációsak, azaz valamely Lagrange-függvény Euler-Lagrange egyenletei,
és megadni az összes ilyen Lagrange-függvényt.
Megkülönböztetjük egymástól a gyenge és erős inverz problémát. A gyenge
probléma esetén konkrét alakú differenciálegyenletek variációs mivoltát
vizsgáljuk, míg az erős probléma célja meghatározni azokat az
egyenleteket, amelyeket valamely ekvivalencia-transzformációval
Euler-Lagrange alakra hozhatunk.
A probléma eredete a 19. században Helmholtz és Sonin munkásságára
vezethető vissza, a gyenge probléma lokális aspektusait a 20. század
közepefele Vainberg és Tonti oldotta meg potenciálelméleti módszerekkel.
A gyenge inverz probléma globális szerkezetének feltárása a 70-es évek
végén és a 80-as évek elején új matematikai technikák - mint például a
variációs bikomplex, a C spektrálsorozat, vagy a véges rendű variációs
szekvenciák - bevezetését igényelte. Ezek fibrált sokaságok feletti jet
nyalábokon értelmezett differenciális komplexek amelyek elemei a
klasszikus variációszámítás objektumainak felenek meg, differenciáljaik
pedig a variációs operátoroknak, például teljes divergenciák, az
Euler-Lagrange leképezés vagy a Helmholtz operátor.
Az említett technikák használata révén lehetőség nyílik a gyenge inverz
probléma globális tárgyalására. A komplexek kohomológiája megadja a
probléma globális megoldását gátoló topológiai obstrukciókat, az
explicit megkonstruálható homotópia-operátorok pedig szisztematikus
megoldását adják a lokális inverz problémának.
Az erős inverz problémának a mai napig nem létezik általános megoldása,
viszont bizonyos speciális részesetei, különösen közönséges
differenciálegyenletek esetén megoldhatóak.
Az előadás célja a gyenge inverz probléma megoldásának, és az ahhoz
szükséges matematikai elméletnek az ismertetése, illetve az erős inverz
probléma kezelhető aspektusainak, azon belüli fontos eredmények
áttekintése.
2022. április 21. (csütörtök) 13:00
Előadó: Roósz Gergő (Wigner FK, ELKH)
Cím: Elektronok és fononok közötti összefonódás
Kivonat |
Előadás
Összefonódási mértékek segítségével a kvantumos rendszerek
korrelációi számszerűsíthetők. Az elektronok és a fononok közötti
csatolás számos érdekes jelenség oka (BCS szupravezetés, Peierls
instabilitás), mégis az elektronok és a fononok közötti
összefonódásról csak a legegyszerűbb modellekben léteznek eredmények.
Az előadás során áttekintem az irodalomban fellehető (numerikus és
közelítő analitikus) eredményeket, majd egy integrálható modellben
(fononok és Luttinger folyadék csatolt rendszerében) meghatározom az
összefonódási entrópiát, a negativitást, és a kölcsönös információt,
és az elektronok sűrűségmátrixára is zárt kifejezést adok meg.
Végezetül a redukált sűrűségmátrix von-Neumann entrópiáját használva
megvizsgálom, hogy a modell milyen fizikai rendszerekre és milyen
paramétertartományban alkalmazható ténylegesen.
2022. március 24. (csütörtök) 13:00
Előadó: Czirják Attila (SZTE Elméleti Fizikai Tanszék, ELI-ALPS)
Cím: A kvantum-interferencia szerepe atomok nagy intenzitású lézerimpulzussal kiváltott alagutazásos
ionizációjában
Kivonat |
Előadás
A fázisteres dinamika és az energiaeloszlás pontos nyomon követése
rávilágít arra, hogy az alagutazásos és a potenciálgát feletti
ionizációs lehetőségek közötti kvantum-interferencia
fontos szerepet játszik a lineárisan polarizált, egyciklusú, közeli
infravörös lézerimpulzus hatására létrejövő atomi ionizációban,
annak ellenére, hogy a lézer csúcsintenzitása alapján tisztán
alagutazásos ionizációt várnánk.
A Wigner-függvényből származtatható kvantum-momentum függvény
segítségével fentiek alapján nem-nulla kezdősebesség adódik
az elektron számára az alagút kijáratánál (szemben az általában
feltételezett 0 értékkel), ami jó összhangban van a legújabb
kísérleti eredményekkel is.
2022. február 24. (csütörtök) 13:00
Előadó: Magashegyi István (SZTE, Elméleti Fizikai Tanszék)
Cím: Szilárdtesttel kölcsönható lézerimpulzus karakterizálása a keltett áramok mérésével: elméleti modell
Kivonat |
Előadás
A csúcstechnológiás femto- illetve attoszekundumos ultrarövid impulzusok alkalmazása
számos területen vezethet áttörő eredményekhez a biológiától kezdve az orvostudományokon
keresztül egészen a mérnöki és ipari alkalmazásokig. Az ultrarövid impulzusok egyik
lehetséges, ígéretes alkalmazása például a szilárdtestbéli elektronok dinamikájának
fényimpulzussal történő manipulálása. Ebben az esetben a lejátszódó kölcsönhatás
egyik alapvető jellemzője az elektronok válaszának az időskálája. Modellek és mérési
eredmények is igazolták, hogy a dielektrikumokban keltett áramok ultragyors
kapcsolási eljárások alapjául szolgálhatnak.
A szilárdtestben keltett áramok detektálása azonban lehetőséget nyújt a keltő impulzus
karakterizálására is. Ebben az esetben a vezetési sáv nagyobb betöltöttsége miatt
érdemesebb félvezetőket vagy vezetőket alkalmazni. A detektáló elektronikus
mérőeszközök időbeli felbontása általában nagyságrendekkel az elektronok válaszának
az időskálája felett van, így ezek mérése nem kivitelezhető ilyen módon. Erre a
problémára nyújthat egy lehetséges megoldást az, ha a detektálásra szánt
szilárdtestből kilépő áramot összegyűjtjük és ezáltal a külső gerjesztő lézerimpulzus
és a keltett töltések kapcsolatát vizsgáljuk.
2020 március 19. (csütörtök) 13:00
Előadó: Roósz Gergő (Insitute of Theoretical Physics, TU Dresden)
Cím: Erősen kölcsönható Majorana fermionok nem középpontosan szimmetrikus szupravezető felületén
Kivonat |
Előadás
A címben említett kölcsönhatás olyan értelemben erős, hogy a fermionokat leíró sáv lapos, a
"kinetikus energia" nulla, ehhez képest bármely véges erősségű kölcsönhatás rendkívül erős.
Az utóbbi években az erősen kölcsönható Majorana fermionok aktív kutatás tárgyát képezik,
mind az elméleti modellek tulajdonságainak megfejtése, mind alkalmas kísérleti realizációk
keresése tekintetében.
Az eladásban ismertetek egy kísérleti elrendezést, amit a
közelmúltban megjelent cikkünkben javasoltunk, és ami az eddigieknél stabilabb
megvalósítását teszi lehetővé az erősen kölcsönható Majorana fermionok rendszerének.
A rendszert jellemző minimális Hamilton operátort egy kétdimenziós négyzetrácson
definiáljuk. Minden rácsponton egy Majorana fermion ül. A rács minden elemi négyzetén
tekintjük a négy csúcsponton található Majorana operátor szorzatát: A Hamilton operátor
ezeknek a négyesszorzatoknak az összege.
A rendszer alapállapota nagymértékben degenerált. A rendszerben nagy számú (a lineáris
kiterjedtséggel arányos számú) mozgásállandó ismert. Ezek közül bizonyos operátorok a
Clifford algebrát generálják. A Clifford algebrák ábrázolása segítségével alsó korlátot adunk
a degeneráció mértékére.
A degenerációt speciális rendszerméretek esetén is vizsgáljuk: kicsi, de tetszőleges alakú
rendszerekre numerikus-egzakt diagonalizációval meghatároztuk az alapállapot
degenerációját. Az egyik irányban 3 vagy 4 rácshely kiterjedésű, a másik irányban
tetszőlegesen hosszú, (azaz létra-szerű) rendszerekre analitikus megoldást találtunk.
Mind az analitikus megoldás, mind a kis rendszerek numerikus megoldása azt mutatja, hogy a
CAR algebrák segítségével kapott alsó korlát a tényleges degenerációval megegyezik.
Befejezésként a rendszer alacsony energiás gerjesztéseit érintjük.
2020. február 13. (csütörtök) 13:00
Előadó: Újfalussy Balázs (Wigner FK, Budapest)
Cím: Nem-konvencionális párállapotok szupravezetőkben
Kivonat |
Előadás
A szupravezetés jelenségét leíró elmélet, a Bardeen–Cooper–Schriffer-elmélet nehézségekbe ütközik inhomogén
rendszerek tárgyalása esetén, amikor például a k hullámszám nem egy jó kvantumszám. Az ilyen rendszerek
leírására
használhatjuk a Bogoljubov–de Gennes-egyenleteket, amit a sűrűségfunkcionál elmélet segítségével
anyagspecifikussá
is tehetünk. Ezen elmélet rövid ismertetése után – ahol kitérek annak relativisztikus általánosítására is -
olyan
rendszereket vizsgálunk, amelyekben a párállapotok valamilyen értelemben nem konvencionálisak. Szó lesz FFLO
állapotokról
mágneses vékonyréteg szupravezetőkben, illetve olyan szupravezetők lehetséges állapotairól, amelyekben a
fém-szupravezető
átalakulást mágneses rend megjelenése kíséri.
2019. december 11. (szerda) 13:00
Előadó: Fehér László (SZTE Elméleti Fizikai Tanszék és
Wigner FK, Budapest)
Cím: Spin Ruijsenaars--Sutherland modellek az U(n) Lie-csoport koérintő nyalábján
definiált bi-hamiltoni rendszer redukciójából
Kivonat |
Előadás
Definiáljuk az U(n) Lie-csoporton mozgó szabad részecskéhez tartozó bi-
hamiltoni hierarchiát, majd ennek szimmetria redukciójával spin Ruijsenaars-
Sutherland típusú integrálható sokrészecske modelleket vezetünk le. Az
előadás elsősorban az arXiv:1908.02467 [math-ph] számú preprinten alapul.
2019. november 28. (csütörtök) 13:00
Előadó: Csonka Szabolcs (BME, Fizika Tanszék)
Cím: Rashba-effektus által indukált spin polarizáció BiTeBr-ban
Kivonat |
Előadás
Spin and momentum of an electron are independent quantum degrees
of freedom. However, when an electron propagates in electric field
coupling between spin and motion is induced. This so-called
spin-orbit coupling is a key resource for spintronic or quantum
electronic setups. Recently a new family of crystals were designed
and realized (BiTeX X=I, Br), where a heavy element (Bi) is placed
in a polar crystal structure, which results a giant Rashba type
spin-orbit interaction.
In this contribution we present experimental examples, to what kind
of peculiar electron transport features the giant Rashba spin-orbit
interaction leads in BiTeBr based nanostructures, like
non-reciprocal current - voltage characteristic or spin
polarization induced by electric field.
2019. október 9. (szerda) 16:00
Előadó: Andrei Zotov (National Research
University Higher School of Economics, Moscow,
Russia and Steklov Mathematical Institute of Russian Academy of
Sciences, Moscow, Russia)
Cím: Quantum-classical dualities in integrable systems
Kivonat |
Előadás
We discuss interrelations between classical many-body
integrable systems of Calogero-Ruijsenaars family and quantum spin
chains (and Gaudin models). We will see that special Lagrangian
submanifolds in the phase space of the classical many-body systems
contain information about spectrum of the corresponding quantum spin
chains.
2019. szeptember 19. (csütörtök) 13:00
Előadó: Czakó Gábor (SZTE, Fizikai Kémiai
és Anyagtudományi Tanszék)
Cím: Új reakcióutak feltárása atomi-felbontású mozifilmekkel
Kivonat |
Előadás
A kémiai reakciók dinamikájának legmélyebb atomi és molekuláris szintű megértése
ma a kémia egyik alapkérdése. Az elméleti kutatás során a fizika törvényeit
alkalmazzuk kémiai rendszerekre, majd a matematika és a modern számítástechnika
eszköztárának felhasználásával végzünk számításokat. A reakciódinamika lépésről
lépésre követi a reakciók lefolyását, így új reakcióutakat tárhat fel és a reakciók
kimenetele is jósolhatóvá válik. Eredményeink formálják a kémiai reaktivitás eddig
ismert alapszabályait, ezáltal lehetővé téve a reakciók irányítását és a kívánt
termékek hatékony előállítását. Kutatásunk során alapvető kémiai reakciók
dinamikáját vizsgáljuk (pl. a szénhidrogének reakciói, illetve a szerves
kémiában jelentős SN2 reakciók mechanizmusának felderítése). Eredményeink
nélkülözhetetlenek a kapcsolódó kísérletek értelmezéséhez, illetve további
mérések tervezéséhez nyújthatnak segítséget.
2019. május 23. (csütörtök) 13:00
Előadó: Forgács Péter (MTA Wigner FK, RMI, Budapest)
Cím: Térben lokalizált nemlineáris gravitációs hullámok -- geonok -- aszimptotikusan anti de Sitter téridőkben
Kivonat |
Előadás
A vakuum Einstein egyenletek néhány olyan figyelemre méltó -
numerikusan megkonstruált - megoldásárol kivánok beszámolni, amelyek
időben periodikusak - így nem sugároznak - és térben lokalizáltak,
aszimptotikájuk pedig anti de Sitter (AdS). Ezen megoldások az
aszimptotikusan AdS téridők instabilitására vonatkozó sejtés
szempontjából is fontosak lehetnek.
2019. április 18. (csütörtök) 13:00
Előadó: Zimborás Zoltán (MTA Wigner FK, RMI,
Budapest)
Cím: Unitér kapuk felbontása és a kvantumszámítás
Kivonat |
Előadás
A kvantumszámítások elméletének egyik alapvető kérdése, hogy sok-qubit
rendszereken definiált unitér operátorokat hogyan tudunk hatékonyan
felbonatni egy adott véges kapukészlet elemeinek minél rövidebb
szorzatára. Az előadás során bemutatok néhány ezzel kapcsolatos
releváns eredményt és technikát - főleg a csoportelméleti ihletésű
módszerekre koncentrálva. Áttekintem a fundamentális téteteleket
(Solvay-Kitaev-tétel, univerzalitási kritérumok) és a praktikus
szempontokat is (releváns kapukészletek, kvantumszimulációkra adaptált
kapufelbontások). Végül felvázolom a legújabb saját eredményeinket is.
2019. március 14. (csütörtök) 13:00
Előadó: Vértesi Tamás (MTA Atomki, Debrecen)
Cím: Hasznos korrelációk kötötten összefonódott állapotokból
Kivonat |
Előadás
A kötötten összefonódottság egy különös formáját képviseli az
összefonódott kvantumállapotoknak. Ezen típusú állapotok olyan gyengén
összefontak, hogy tiszta formában végtelen számú példányukból sem
nyerhető ki összefonódottság. Ennek ellenére hasznosnak bizonyulnak
olyan alkalmazásokban, mint a kvantumos kulcskiosztás, adatrejtés,
vagy biztonságos véletlenszámok előállítása. Ebben az előadásban
megmutatjuk, hogy a kötötten összefonódott állapotokat
Bell-egyenlőtlenségek sértésére is lehet használni. Ez egyúttal
ellenpéldát ad Asher Peres 1999-es sejtésére. Az ilyen korrelációk a
kvantuminformatika eszközfüggetlen alkalmazásaiban is hasznosulhatnak.
2019. február 19. (kedd) 16:00
Előadó: Asbóth János (MTA Wigner FK, SZFI, Budapest)
Cím: Mire használhatók a nemhermitikus Hamilton-operátorok: tömbi
topologikus invariáns mérése veszteségeken keresztül
Kivonat |
Előadás
Topological insulators have Hamiltonians with bulk topological
invariants, which control the interesting processes at the surface of
the system, but are hard to measure directly. We have found a way to
measure the bulk topological invariant (winding number) of
one-dimensional topological insulator Hamiltonians (with chiral
symmetry): it is given by the displacement of a single particle,
observed via losses[1]. Losses represent the effect of repeated weak
measurements on one sublattice only, which interrupt the dynamics
periodically. When these do not detect the particle, they realize
negative measurements. Our repeated measurement scheme covers both
time-independent and periodically driven (Floquet) topological
insulators, with or without spatial disorder. In the limit of rapidly
repeated, vanishingly weak measurements, it applies to non-Hermitian
Hamiltonians, such as the lossy Su-Schrieffer-Heeger model[2]. Contrary
to intuition, the time needed to detect the winding number can be made
shorter by decreasing the efficiency of the measurement. Our scheme has
since been used to measure the bulk topological invariants of a
discrete-time quantum walk on photons[3].
[1] T Rakovszky, JK Asboth, and A Alberti, Phys. Rev. B 95, 201407 (2017).
[2] MS Rudner and LS Levitov, Phys. Rev. Lett. 102, 065703 (2009).
[3] X Zhan et al, Phys. Rev. Lett. 119, 130501 (2017)
2019. február 14. (csütörtök) 13:00
Előadó: Diósi Lajos (Wigner FK, RMI)
Cím: Kvantumkontroll és féligklasszikus kvantumgravitáció
Kivonat |
Előadás
Nincs elfogadható kvantumgravitációs elméletünk.
Helyette a féligklasszikus elméletet használjuk,
ahol a téridő klasszikus (értsd: kvantálatlan)
marad. A hybrid kvantum-klasszikus csatolás azonban
akauzális, sérti a kvantumelmélet linearitását és a
Born valószínűségi szabályt is. Az anomáliák eltűnnek,
ha a kvantum mérés-visszacsatolás pl. kvantum-optikából
ismert mechanizmusára építve módosítjuk a jólismert
átlagtér csatolást. A newtoni határeset kidolgozható.
Penrose és az előadó korábbi, gravitációs spontán
hullámfüggvény-kollapszus elméletére vezet.
2018. december 12. (szerda) 13:00
Előadó: Iglói Ferenc (MTA Wigner FK, Budapest és SZTE
EFT)
Cím: Kvantumos relaxáció és metastabilitás optikai rácson ülő atomok rendszerében optikai rezonátor
által keltett hosszú-hatótávolságú kölcsönhatás esetén
Kivonat |
Előadás
A kvantumtechnológia fejlődésével ultrahideg körülmények között semleges
gázok atomjait lehet egy optikai rácsra helyezni,
mely atomok között elsőszomszéd kölcsönhatások (hopping és onsite taszítás)
alakulnak ki. Amennyiben a teljes rendszert egy finoman hangolható optikai
rezonátor belsejében helyezzük el, úgy az hosszú-hatótávolságú kölcsönhatást
is kelt az atomok között, és a rendszer alapállapotát a kölcsönhatások
versengése és a kvantumos fluktuációk jelenléte határozza meg. A kísérletek
szerint a rendszer egzotikus fázisokkal - szuperfolyadék (superfluid - SF),
szu- perszilárd (supersolid - SS), sürüséghullám (density wave - DW) - rendelkezik
és érdekes dinamikát mutat. A kísérleti háttér rövid vázolása után a jelen
előadásban elméleti eredményeket mutatunk be. Az atomokat kemény-magú bozonokkal
írjuk le és ezek egydimenziós rendszerét tekintjük rövid- és hosszú-hatótávolságú
kölcsönhatás jelenlétében. A termodinamikai határesetben mind az egyensúlyi
fázisdiagramot, mind a hirtelen paraméter változtatással járó (idegen szóval kvencs)
kvantumos relaxációs folyamatokat egzaktul meghatározzuk. A DW → SF kvencs esetén
remanens DW rendet találunk, míg a fordított SF → DW kvencs esetén DW rend alakul
ki a megmaradó SF renddel együtt, mely dinamikai módon generált szuperszilárd
állapotot jelent.
[1] B. Blaß, H. Rieger, G. Roósz and F. Iglói, Phys. Rev. Lett. 121, 095301 (2018)
[2] F. Iglói, B. Blaß, G. Roósz and H. Rieger, Phys. Rev. B 98, 184415 (2018)
2018. november 8. (csütörtök) 13:00
Előadó: Bíró Tamás Sándor (MTA Wigner FK, Budapest)
Cím: Az Unruh hőmérsékletről
Kivonat |
Előadás
Az Unruh hőmérséklet egy látszólagos hőmérséklet állandó gyorsulású
rendszerekben. Először különböző utakat tekintek át, amelyek ehhez a
fogalomhoz vezetnek a kvantum elmosódástól a folytonosan változó Doppler
effektusig, majd az eredményt összehasonlítom a gyorsuló töltés
elektromágneses sugárzási spektrumával. Néhány nehézion fizikai
alkalmazás ismertetése zárja a sort.
2018. október 25. (csütörtök) 13:00
Előadó: Magashegyi István (SZTE, Elméleti Fizikai Tanszék)
Cím: Töltéshordozók fénnyel kontrollált dinamikája
Kivonat |
Előadás
Az ultrarövid fényimpulzusok anyaggal történő kölcsönhatásának vizsgálata
számos érdekes fizikai jelenségre mutatott rá. Ilyen impulzusok egy lehetséges,
ígéretes alkalmazása pl.~a szilárdtestbeli elektronok dinamikájának
fényimpulzussal történő manipulálása. Fémek esetén az áramok időbeli
integráljából számolható töltés és a gerjesztő fényimpulzus tulajdonságainak
a kapcsolata lehet izgalmas kérdés.
Vezetők esetén, ha a megfelelően hangolt lézerimpulzus olyan gyenge,
hogy az indukált sávátmenetek elhanyagolhatók, akkor a lejátszódó folyamatot
a vezetési sávbéli elektronok áramának változásai dominálják. Egyelektron
közelítésben kvadratikus diszperziós relációt feltételezve a sáv alján lévő
elektronok tekinthetők egy adott irányba terjedő kvantummechanikai síkhullámnak.
A teljes szilárdtest válaszát a különböző hullámszámvektorú szimulációk során
kapott eredmények Fermi statisztika szerinti felösszegzésével kaphatjuk meg.
A tapasztalataim azt mutatják, hogy kiáramló össztöltés és a lézerimpulzus
kapcsolatának numerikus időintegrál alapján történő meghatározása nehezen
optimalizálható. Az előadásomban egy olyan analitikus megközelítést mutatok
be amelynek segítségével a szóban forgó időintegrál a hullámfüggvényből
egzaktul számolható.
2018. október 15. (hétfő) 11:00
Előadó: Horváth Dezső (MTA Wigner Fizikai Kutatóközpont, Budapest
és MTA Atomki, Debrecen)
Cím: A CPT-invariancia kísérleti ellenőrzése a CERN-ben
Kivonat |
Előadás
A részecskefizika egyik legalapvetőbb szimmetriája a CPT-invariancia, amelynek egyenes
következménye, hogy részecske és antirészecske tulajdonságai töltésük előjelén kívül teljesen
azonosak. Ennek látszólag ellentmond, hogy a világegyetem általunk belátható részében nincs
antianyag jelentős mennyiségben. A részecskefizika számos jelenlegi rejtélyének egyike, hova
tűnhetett az anyaggal feltehetően azonos mennyiségben keletkezett antianyag az ősrobbanás után,
milyen különbség lehet közöttük. A CERN csaknem 20 éve megépítette fellengzősen
Antianyaggyárnak keresztelt antiproton-lassító (Antiproton Decelerator, AD) berendezését a kérdés
tisztázására jó néhány kísérlettel, és nemrégiben üzembe helyezett egy űrbeli detektort (AMS2) a
Nemzetközi Űrállomáson a kozmikus sugarak antirészecskéinek észlelésére. Az előadásban az
anyag-antianyag szimmetria kísérleti vizsgálatainak leírása után kitérek az antianyag valódi,
lehetséges és lehetetlen gyakorlati alkalmazásaira.
2018. szeptember 27. (csütörtök) 16:00
Előadó: Maxime Fairon (Department of Applied Mathematics,
University of Leeds)
Cím: Understanding the Calogero-Moser system with double Poisson brackets
Kivonat |
Előadás
The starting point for this talk is the well-known
definition of the phase space for the complex Calogero-Moser system
given by Wilson in terms of matrices. I will show that it is natural
to reconsider the Poisson geometry of this space using only symbols
representing these matrices. By doing so, we are led to the definition
of a double bracket on the path algebra of a very simple quiver. I
will explain how this falls within the general formalism of Van den
Bergh which associates a double Poisson algebra to an arbitrary
quiver. Going backward, we will look at the latter structure for some
extended cyclic quivers and link it to integrable systems of
Calogero-Moser type, following an approach of Chalykh and Silantyev.
Time allowing, I will sketch how to obtain the same results in the
relativistic case.
2018. szeptember 25. (kedd) 10:00 (Riesz terem)
(közös szeminárium az Analízis Tanszékkel)
Előadó: Fumio Hiai (Tohoku University, Sendai, Japan)
Cím: Different quantum $f$-divergences in quantum systems
Kivonat | Előadás
This talk surveys recent developments on quantum
$f$-divergences in quantum systems. We discuss three different
quantum $f$-divergences of standard, maximal and minimal (or
measured) types, as well as Rényi type quantum divergences,
first in the finite-dimensional matrix setting and then in
the von Neumann algebra setting. Standard $f$-divergences were
formerly studied by Petz in a bit more general formula with
name quasi-entropy, whose most familiar one is the relative
entropy initiated by Umegaki and extended to general
von Neumann algebras by Araki. We present basic properties of
quantum $f$-divergences and in particular discuss the equality
case in their monotonicity inequality under quantum operations.
Part of this talk is joint work with Milán Mosonyi.
2018. május 8. (kedd) 10:00 (Rédei terem)
(közös szeminárium az Analízis Tanszékkel)
Előadó: Martin Hallnäs (Chalmers University of Technology and University of Gothenburg)
Cím: Exceptional orthogonal polynomials and quasi-invariance
Kivonat |
Előadás
The focus of my talk will be on systems of polynomials given in terms
of Wronskians of classical Hermite polynomials and naturally labelled
by partitions. For the special class of so-called double partitions,
Gomez-Ullate, Grandati and Milson showed that the corresponding
polynomials are orthogonal and dense in the space of all polynomials
with respect to a certain inner product, but in contrast to their
classical counterparts have some degrees missing (so-called
exceptional orthogonal polynomials). I will describe how their results
can be generalised to all partitions by using the notion of
quasi-invariance and considering complex contours of integration and
non-positive, but Hermitian, inner products. If time permits, I will
also indicate a multivariate generalisation of some of these results.
The talk is based on joint work with W.A. Haese-Hill and A.P. Veselov
2018. április 12. (csütörtök) 13:00
Előadó: László András (MTA Wigner FK, RMI, Budapest)
Cím: Általános relativisztikus korrekciók becslése müon g-2 és EDM kísérletekhez
Kivonat |
Slides
Az elmúlt hetekben egy kéziratsorozat látott napvilagot az arXiv-on, Morishima, Futamase es Shimizu tollából.
Azt állítják, hogy az általános relativitáselmélet okozhat egy eddig figyelembe nem vett korrekciot a müon g-2
mérésekben.
Válaszul más szerzők amellett érveltek, hogy az effektus nem lehet ilyen nagy. További szerzők szerint,
az effektus konkrétan nem létezik. Mindez azt mutatja, hogy viszonylag nehéz első elvekből, filozófiai alapon
megmondani,
hogy az áltrel mekkora korrekciót adhat a spintranszporthoz, mely a g-2 kísérletek alapja. A spintranszportot
a Fermi--Walker-differenciálegyenlet írja le, mely speciális relativisztikus határesetben a Thomas-precessziót
okozza.
Az előadásban bemutatjuk, hogy miképpen lehet Lorentz geometria szempontjábol, közelitésmentesen kiszámolni az
effektust.
Kiszámoljuk továbbá, hogy a kísérletben is használt elektromágneses tárológyűrűvel együtt milyen korrekció
várható. Kiderül,
hogy az áltrel valóban ad elsőrendű korrekciót a g-2 méréshez, azonban ez bőven a jelenlegi mérési pontosság
alatt van.
Azonban a hasonló jellegű elektromos dipólmomentum (EDM) mérésekhez ad elvben mérhető korrekciót, mely ráadásul
nagyobb
mint a Standard Modellből jövő várakozás. A számolás az arXiv:1803.01395 kéziratban van részletezve.
2018. március 22. (csütörtök) 16:00
Előadó: Gyenis
Balázs (MTA BTK Filozófiai Intézet, Budapest)
Cím: Az egyensúly felé törekvés és a valószínűség interpretációja
Kivonat |
Előadás
Két gázt összekeverve hőmérsékletük kiegyenlítődik. Az előadásban egy,
ezt a jelenséget mechanikailag alátámasztani próbáló
bizonyítás-kísérletet mutatunk be és elemzünk fizikai, történeti, és
filozófiai szempontból. Kiindulópontunk Maxwell egy 1860-as cikkében
adott bizonyításának jóindulatú rekonstrukciója, amely nem csak megelőzi
Boltzmann - a tudománytörténészek által elsőnek gondolt - ilyen irányú
próbálkozásait, de elegánsabb és egyszerűsége folytán beemelhető lenne
akár a középiskolai szintű fizika oktatásba is, ezért tudománytörténeti
jelentőségétől függetlenül is érdemes vele megismerkedni. Az előadás
második felében a bizonyítás-kísérlet alapjául szolgáló problematikus
valószínűségi feltevéseket és azok lehetséges értelmezéseit vizsgáljuk meg.
2018. március 8. (csütörtök) 14:30
(közös szeminárium a Geometria Tanszékkel)
Előadó: Bozidar Jovanovic (Mathematical
Institute SANU, Belgrade, Serbia)
Cím: Symmetries and noncommutative integrability
Kivonat | Előadás
We will outline the proof of the theorem on noncommutative integrability of Hamiltonian
systems introduced by Nekhoroshev and Mishchenko and Fomenko.
In the second part of the lecture we shall briefly present applications of noncommutative
integrability in natural mechanical systems and geodesic flows on homogeneous
spaces.
2018. február 22. (csütörtök) 13:00
Előadó: Surján Péter (ELTE TTK, Kémiai Intézet)
Cím: Divergens perturbációs sorok felösszegzéséről
Kivonat |
Előadás
Perturbation theory aims to approximate the eigenvalues of a linear
operator H in form of a power series
by splitting this operator as H = H_0 + W, and knowing
the eigenvalues and eigenvectors of the zero order operator H_0.
In this seminar, we investigate the following issues:
1) is it possible to convert a divergent PT to a convergent
one by redefining the partitioning, that is by redefining
the zero order Hamiltonian?
2) Knowing the members of the divergent series, is it possible
to set up a mathematical tool to estimate the exact physical
result from the partial sums?
3) Can the mathematical method of analytical continuation be used
as an aid for point 2)?
4) If the answer to point 3) is affirmative, what kinds of
technics of analytical continuation are promising?
2018. január 30. (kedd) 13:00
Előadó: Keresztes Zoltán (SZTE, Elméleti Fizikai Tanszék)
Cím: Precesszáló kompakt kettősök szekuláris dinamikája
Kivonat |
Előadás
Mivel az eddig felfedezett gravitációs hullámok összeomló kettősökből származnak,
ezért azok fejlődésének pontos leírása mind fontos és időszerű.
Az evolúció bespirálozási szakaszát három időskála jellemzi.
A legrövidebb a radiális időskála, ami alatt a redukált tömegű objektum egy teljes
radiális periódust tesz meg a központi össztömeg körül. Egy második időskála akkor jelenik meg,
amikor a spinek és a pálya-impulzusmomentum nem párhuzamosak egymással. Ekkor a spin és a
pálya-impulzusmomentum vektorok precesszió-szerű mozgást végeznek. Ez meghatároz egy precessziós
időskálát, amely sokkal hosszabb, mint a pálya periódus. A harmadik az az időskála, ahol a
gravitációs sugárzási visszahatás jelentőssé válik. Mi a dinamikát a precessziós időskálán
tárgyaljuk, ahol az evolúciós egyenletek egy radiális periódusra vett átlagai vehetőek,
ami a dinamika leírását jelentősen egyszerűsíti. A származtatott konzervatív szekuláris
evolúciós egyenletek második poszt-newtoni rendű pontosságúak és tartalmazza a vezető rendű
spin-pálya, spin-spin és tömeg kvadrupól-monopól kölcsönhatásokat. Az elsőrendű
differenciálegyenlet rendszer változói a spin és a pálya-impulzusmomentum vektorok polár és
azimutális szögei, valamint a periasztron szöge. Szemben a pillanatnyi dinamikával a szekuláris
dinamika autonóm. A rendszer megbízhatóan írja le a dinamikát olyan időskálán, ami néhány
radiális periódustól számos precessziós periódusig tart, de kisebb, mint a sugárzási visszahatás
időskálája. Az analitikus egyenleteket alkalmazzuk a spin flip-flop jelenség tanulmányozására,
amelyet korábban numerikus relativitáselméleti módszerekkel találtak. Kiderül, hogy a rendszer
nagyon hasznos a spin flip-flop effektus paraméter terének a feltérképezésében.
2017. december 14. (csütörtök) 13:00
Előadó:
Fülöp
Tamás
(BME Energetikai Gépek és Rendszerek Tanszék)
Cím:
Valószínűségi áram a nulla spinű relativisztikus kvantummechanikában
Kivonat | Előadás
Az előadás a nulla spinű relativisztikus kvantummechanika egy olyan megfogalmazását ismerteti,
ahol a természetes módon adódó megmaradó áram pozitív definit. E valószínűségi áramhoz kötődően
egy szokásos, Hilbert-teres egyrészecske-leírást kapunk. A szabad eset ekvivalensnek bizonyul
a Klein-Gordon-egyenleten alapuló megfogalmazással, nemszabad esetben azonban sérül az
ekvivalencia. A másodkvantált esetben a nulla spinű részecskék újfajta kölcsönhatásaira
és önkölcsönhatásaira nyílhat mód.
2017. november 16. (csütörtök) 16:30
Előadó:
Böhm Gabriella
(Wigner FK, RMI, Budapest)
Cím:
Kvantumszimmetriák
Kivonat | Előadás
A kvantumtérelmélet Haag és Kastler nevéhez fűződő axiomatikus megközelítése a
Minkowski-téridő kauzálisan zárt tartományaihoz rendelt C*-algebrákra (az ott lokalizált
megfigyelhető mennyiségekre) tesz feltevéseket. Ezek fennállása esetén a fizikailag
relevánsnak tekintett ábrázolások egy kategóriát (az úgy nevezett Doplicher--Haag--Roberts,
vagy röviden DHR-kategóriát) határoznak meg, gazdag további szerkezettel.
Ebben a kontextusban "szimmetria" alatt egy olyan algebrai struktúrát (csoportot vagy
alkalmas általánisítását) értünk, aminek ábrázolási kategóriája ekvivalens a
DHR-kategóriával.
Doplicher és Roberts munkája nyomán tudjuk, hogy 3+1 dimenzió esetén a szimmetria egy
(izomorfizmus erejéig egyértelmű) kompakt csoport. Alacsonyabb dimenzióban azonban olyan
tulajdonságok fordulnak elő, amelyek kizárják a csoport szimmetriát. Itt jutnak szerephez
az ún. "kvantumszimmetriák" (Hopf-algebrák és variánsaik) melyek a csoportok
általánosításainak tekinthetők és alkalmasak az alacsony dimenziós kvantumtérelméletek
szimmetriájának leírására.
Az előadásban áttekintést szeretnénk adni a fenti programról, a precíz definíciók és
tételek idézése helyett szemléletes kép kialakításával. Egyik érintett terület ismerete
sem feltétele az elmondandók követésének.
2017. szeptember 21. (csütörtök) 13:00
Előadó: Kálmán Orsolya (Wigner FK, SZFI,
Budapest)
Cím: Mérések által indukált nemlineáris transzformációk kvantuminformatikai alkalmazási lehetőségei
Kivonat | Előadás
Mérésekkel és a mérési eredmények felhasználásával történő posztszelekció révén létrejövő
nemlineáris kvantumos dinamika kvantuminformatikai felhasználási lehetőségeivel foglalkozom az előadásban. Az
ilyen típusú sémáknak egy qubit-sokaságon történő iteratív alkalmazása során a kapott dinamika nagyon érzékeny a
kezdeti qubit-állapotra és megmutatható, hogy bizonyos esetekben a rendszer a kezdeti állapotától már néhány
iterációs lépés után gyorsan eltávolodik. Egy általunk vizsgált kísérleti sémában például megmutattuk, hogy
olyan nemlineáris transzformáció valósítható meg, amely alkalmas arra, hogy kezdetben közeli állapotokat
egymásra ortogonális állapotokba transzformáljon, amelyek azután már projektív méréssel megkülönböztethetők
egymástól, így a séma felhasználható állapot-megkülönböztetésre [1]. Az ortogonalizáló tulajdonsággal rendelkező
protokollok egy további érdekes felhasználási lehetőségét is vizsgáltuk, amelyet
kvantumállapot-összepárosításnak („quantum state matching”) neveztünk el. Ennek lényege, hogy egy alkalmasan
megválasztott nemlineáris transzformáció iterálása segítségével egy ismeretlen állapotról el tudjuk dönteni,
hogy az egy referencia-állapot előre definiált sugarú környezetében van-e, ugyanis a nemlineáris transzformáció
speciális tulajdonságainak köszönhetően az ismeretlen állapot vagy a referencia-állapothoz, vagy az arra
ortogonális állapothoz kerül minden iterációs lépéssel közelebb [2].
[1] J. M. Torres, J. Z. Bernád, G. Alber, O. Kálmán, T. Kiss, Phys. Rev. A 95, 023828 (2017)
[2] O. Kálmán, T. Kiss, arXiv:1708.03610
2017. szeptember 14. (csütörtök) 13:00
Előadó: Vattay Gábor (ELTE TTK Komplex Rendszerek Fizikája Tanszék)
Cím: A transz-Turing gép
Kivonat | Előadás
A kvantum számítógép az elmúlt néhány évben átkerült a tisztán intellektuális világból
a technológiai evolució valóságába. Az elsőként elkészült berendezés (D-Wave) nem
hasonlít arra, amit a kvantum algoritmusok kutatói megálmodtak. A legdrámaibb különbség,
hogy az architektúra nem logikai lépéseket hajt végre és ilyen formán nem Turing elven
működik. Míg az algoritmikus számítógép tudomány számára ez nem kielégítő és továbbra
is várakozással néz a tökéletes kvantum logikát megvalósító architektúrák felé,
addig előadásomban amellett érvelek, hogy ez a fejlemény logikusan következik a statisztikus
fizika és a számításelméleti komplexitás közötti szoros kapcsolatból. Az új Turing utáni architektúrát
maguk a megoldandó feladatok kényszerítik ki. A kvantum éra eljövetelével nem csak a számítógépeink
fizikai elveit cseréljük újakra, hanem egyben a számító-gép fogalmát is lecseréljük.
2017. május 18. (csütörtök) 13:00
Előadó: Van Leeuwen-Polner Mónika (SZTE, Alkalmazott és Numerikus Matematika Tanszék; ELI-Alps)
Cím: Ultrarövid elektromágneses impulzusok szórása két párhuzamosan elhelyezett fémrétegen: A sugárzási
visszahatás és az időkésleltetés szerepe
Kivonat | Előadás
Két párhuzamosan elhelyezett vékony fémrétegre beeső, néhány ciklusú lézerimpulzus reflexióját és
transzmisszióját vizsgáljuk. A felületi áramsűrűséggel modellezett rétegek három különböző törésmutatójú
dielektrikum közé vannak beágyazva. A felületi áramok és a teljes sugárzási tér dinamikáját a Maxwell-Lorentz
egyenletek csatolt rendszere írja le. A modellben fellépő idő késleltetés függ a lézer impulzus beesési
szögétől, a dielektrikumok törésmutatóitól és a két réteg közötti távolságtól. Az előadás során áttekintjük az
eredő csatolt késleltetett differencia-differenciálegyenlet rendszer analitikus megoldását.
2017. április 13. (csütörtök) 13:00
Előadó: Görbe Tamás Ferenc (SZTE, Elméleti Fizikai Tanszék)
Cím: Calogero-Ruijsenaars típusú integrálható rendszerek
Kivonat | Előadás
Az előadásban áttekintjük a Calogero-Ruijsenaars típusú integrálható rendszereket és az ezekhez kapcsolódó
doktori munkám eredményeit.
2017. április 5. (szerda) 15:00
Előadó: Pitrik József (BME, Analízis Tanszék)
Cím: Entrópiák és divergenciák
Kivonat | Előadás
Az előadás során áttekintünk néhány fontos entrópia és divergencia fogalmat. Megmutatjuk, hogy milyen
matematikai, illetve fizikai problémafelvetés motiválta bevezetésüket, és milyen jellemző tulajdonságokkal
bírnak. Igyekszünk néhány példán szemléltetni néhány további alkalmazásukat.
2017. március 29. (szerda) 15:00
Előadó: Simon Ruijsenaars (Department of Applied Mathematics, University of Leeds, UK)
Cím: A relativistic conical function and its descendants
Kivonat | Előadás (angolul)
We first review one-dimensional potential scattering, tying in the repulsive and attractive potentials
$$g(g-1)/\sinh^2(x),\ \ \ -g(g-1)/\cosh^2(x),\ \ \ g>1,$$
with the conical/Mehler function specialization of the hypergeometric function. After linking this to the
hyperbolic $N$-particle Calogero-Moser systems of $A_{N-1}$ type, we present our relativistic version of the
latter. Specializing again to the reduced 2-particle setting, we sketch results concerning a relativistic
generalization of the conical function. In particular, we discuss how it supplies unitary eigenfunction
transforms for the repulsive and attractive cases, and how its asymptotics results in scattering amplitudes
satisfying the Yang-Baxter equations. Other topics touched on are product formulas, $SL(2,Z)$ and Cherednik's
DAHA (double affine Hecke algebra). Some of the results involve joint work with Martin Hallnäs and Steven
Haworth.
2017. március 16. (csütörtök) 13:00
Előadó: Balog János (Wigner FK, RMI)
Cím: Effektív potenciál a relativisztikus szóráselméletben
Kivonat | Előadás
Az utóbbi években sikerült az alapvető kölcsönhatásokból származtatni
a magfizikai nukleon-potenciált, rács QCD mérésekkel. Ez motiválta
vizsgálatainkat, amelyekben az analóg kérdéseket alacsony dimenziós, megoldható térelméleti modellekben
vizsgáltuk.
Az előadásban bemutatjuk a kvantummechanikai inverz szórás módszerét
és alkalmazzuk egy egyszerű példában: az 1 + 1 dimenziós Sine-Gordon
modellben.
2017. február 23. (csütörtök) 13:00
Előadó: Tóth Gábor Zsolt (Wigner FK, RMI)
Cím: Megmaradó áramok konstrukciója mértékelméletekben rögzített háttér esetén
Kivonat | Előadás
Ismert, hogy téridőszimmetriával rendelkező
rögzített gravitációs térben propagáló anyagmezőkhöz nemcsak a Noether tétel
alkalmazásával lehet megmaradó áramokat konstruálni,
hanem az Einstein-Hilbert energia-impulzus tenzor felhasználásával is.
Bár a két konstrukció bizonyos értelemben ekvivalens eredményt ad,
a második konstrukció gyakran hasznosabb. Az előadásban ennek a konstrukciónak
a Noether-féle értelemben vett általános mértékelméletekre való kiterjesztését ismertetem,
továbbá illusztrációként konkrét példákat mutatok be.
2017. február 9. (csütörtök) 13:00
Előadó: Barna Imre (Wigner FK, RMI; ELI-Alps)
Cím: Hélium ionizációja
Kivonat
Előadásomban összefoglalom a hélium egyszeres és kétszeres ionizációjáról szóló
eddigi munkáimat nehéz ionok, pozitronok, antiprotonok és rövid erős
lézerimpulzusok terében.
Elméleti leírásként egy időfüggő ab-initio módszert használtam, ahol az
alkalmazott bázist Slater függvényekből és reguláris Coulomb hullámcsomagokból
építettem fel.
Szemináriumok 2016-ban
2016. december 1. (csütörtök) 13:00
Előadó: Vecsernyés Péter (Wigner FK, RMI)
Cím: Mi történik egy mérés során? - Weinberg válaszol
Kivonat | Előadás
A kvantummechanika méréselméleti dogmái szerint méréskor "fölfüggesztődik" a vizsgált részrendszer unitér
időfejlődése, és a részrendszer a mért mennyiség sajátállapotába (szelektív mérés), avagy az általa generált
abeli részalgebrájába (nem-szelektiv mérés) "ugrik". Ezek az "ugrások" teljesen pozitív leképezések a
részrendszeren,
melyek egy-egy értelmű kapcsolatban vannak egy nagyobb rendszer unitér leképezéseinek a vizsgált
részrendszerre történő megszorításával.
Ezért fölmerül a kérdés: lehet-e egy nem-szelektív mérés "eredménye" dinamikai folyamat, azaz teljesen pozitív
leképezések időparaméterezett félcsoportjának hatására időben aszimptotikusan előálló állapot?
A szemináriumon Weinberg konstruktív igenlő válaszát és a szükséges fogalmakat, korábbi eredményeket
ismertetjük.
Irodalom:
Weinberg írása
2016. november 11. (péntek) 13:00 (Intézeti szeminárium)
Előadó: Heiko Rieger (Theoretische Physik, Universitat des Saarlandes, az SZTE díszdoktora /2016./)
Cím: Biophyics of Killing - Theory and Experiment
Kivonat (angolul)
Cytotoxic T lymphocytes and natural killer cells are the main cytotoxic killer cells of the human body to
eliminate pathogen-infected or tumorigenic cells. Various processes are involved in a successful killing
event: activation of the killer cell, migration and search for the target, formation of a synapse and
polarization upon contact with the target, transport of cytotoxic agents towards the synapse, and finally
elimination of the target via necrosis or apoptosis. In this talk I will review various biophysical aspects of
killing that we studied in collaboration with immunologists.
Topics include the analysis of search strategies of migrating killer cells; the efficiency of the spatial
organization of the cytoskeleton for search problems occurring in intra-cellular cargo transport; the analysis
of different killing strategies inducing necrosis or apoptosis; the modulation of the intracellular calcium
homoeostasis by mitochondria relocation towards the synapse; and the mechanistic understanding of the
molecular motor driven cytoskeleton rotation towards the synapse during polarization.
2016. november 10. (csütörtök) 13:00
Előadó: Vibók Ágnes (Debreceni Egyetem, Elméleti Fizikai Tanszék)
Cím: Fénnyel indukált ultragyors dinamikai folyamatok molekuláris
rendszerekben
Kivonat | Előadás
A kónikus keresztezôdéseken, vagy másképpen
nevezve elektronikus degeneranciákon keresztül lejátszódó
dinamikai folyamatok a számos elektronállapot és magrezgések erôs csatolódása miatt eredendôen
nemadiabatikusak.
A keresztezôdések helyén a nemadiabatikus
csatolás szingulárissá válik, ami számos statikai és dinamikai hatás
megjelenését váltja ki. Ilyen például a topológiai Longuet Higgins-
vagy más néven a Berry-fázis megjelenése is.
Ilyen keresztezôdések lézerfény segítségével is létrehozhatók, akár álló, akár pedig haladó
lézerhullámokkal. Megjelenésük egy új, fizikailag érdekes
lézer-anyag kölcsönhatás kialakulásához vezet, amelynek hatására jelentôsen megváltoznak és szabályozhatóvá
válnak a kialakuló dinamikai folyamatok.
2016. november 3. (csütörtök) 13:00
Előadó: Apagyi Barnabás (BME, Elméleti Fizikai Tanszék)
Cím: Inverz kvantum szórás
Kivonat |
Előadás
Az inverz kvantum szórás elmélete egyértelmű kapcsolatot létesít a szórásadatok (pl. fázistolás-sorozat) és a
szórást létrehozó kvantum-mechanikai potenciál között. A szórás (vagy spektrál) adat az input mennyiség, a
potenciál az output termék. Az elmélet ezen ok-okozati kapcsolat megfordítását szigorú matematikai eszközök
használata révén éri el (így pl. paraméter-illesztés, vagy minimalizálás nem tartozik az eszköztárba). Az
előadásban áttekintjük az inverz szórás elmélet fejlődését és alkalmazásainak körét. Tárgyaljuk a jól ismert
fix impulzus-momentum (Gelfand-Levitan-Marchenko) és fix energia (Newton-Sabatier) melletti inverz szórást,
valamint egy új fix-energiás módszert, amely az előzők egyesítésének tekinthető véges hatótávolságú
potenciálok meghatározására.
2016. október 27. (csütörtök) 13:00
Előadó: Patkós András (ELTE, Atomfizikai Tanszék)
Cím: A sötét anyag (és a sötét energia) kihívása
Kivonat |
Előadás
A sötét anyag csillagászati megnyilvánulásainak rövid számbavétele után áttekintem a jelenleg
legelterjedtebben
vizsgált potenciális összetevői kutatásának helyzetét. Elemzem, hogyan újult meg a gravitációs hullám
létezésének felfedezése nyomán a
sötét makroszkopikus kompakt objektumok utáni érdeklődés. A részecskefizikai jelöltek közül a Nagytömegű
Gyengén Kölcsönható Részecskék (WIMP)
és az Axionszerű Könnyű Részecskék (ALP) kutatásának elméleti hátterét és aktuális helyzetét mutatom be.
2016. október 13. (csütörtök) 13:00
Előadó: Iglói Ferenc (MTA Wigner FK, SZTE Elm. Fiz. Tansz.)
Cím: Hogy kerül a topológia a szilárdtestfizikába? A 2016. évi fizikai Nobel-díj
Kivonat |
Előadás
2016-ban a fizikai Nobel-díjat DJ Thouless, FDJ Haldane és JM Kosterlitz kapták, "a topologikus
fázisátalakulások és a topologikus fázisok elméleti felfedezéséért". Az előadásban áttekintjük a Nobel-díjjal
jutalmazott, 1970-es és 1980-as évekből származó eredményeket. Megmutatjuk, hogy miért voltak ezek meglepőek,
hogyan építettek ezekre a 2000-es években kivirágzott topologikus szigetelők elméletében, és hogyan vezethet
ez az út a kvantumszámítógép megalkotásához.
2016. október 6. (csütörtök) 13:00
Előadó: Varró Sándor (MTA Wigner FK, ELI-ALPS)
Cím: A foton fázisoperátora mint Haar-integrál a Blaschke-csoporton
Kivonat |
Előadás
A harmonikus oszcillátor kvantált amplitúdójára (amely pl. egy fotonmódust is leírhat) nemrég egy új
polárfelbontást (exponenciális fázisoperátort), s ennek alapján egy új, „reguláris fázisoperátort” (kvantum
szögváltozót) vezettünk be Fourier-korrespodenciával [1]. Meghatároztuk az exponenciális fázisoperátor
sajátállapotait is, amelyekről kiderült, hogy a komplex egységkörlap belsejében paraméterezett SU(1,1)
koherens állapotok Holstein-Primakoff-típusú realizációi. E formalizmus keretében a sugárzási tér kvantumos
fáziseloszlásai [1], valamint a fotonszám-fázis Weyl-korrespondencia, és a Wigner-függvények is természetes
módon definiálhatók [2].
Az előadásban, a fenti előzmények ismertetése után, a reguláris fázisoperátor időfejlődését elemezzük, és
bebizonyítjuk, hogy a teljes fizikai fázis periodikus, amelyről megmutatjuk, hogy két nemkorlátos tag összege
[3]. Egyrészt az oszcillátor (triviális) dinamikai fáziscsökkenése egy lineáris negatív járulékot ad, másrészt
ehhez adódik még egy lépcsőszerűen növekvő rész is (lásd az 1. ábrát). Az utóbbi egy pozitív operátorértékű
Haar-integrál a Blaschke-csoporton (amely az SU(1,1) csoport egy speciális paraméterezése; esetünkben az
egységkörlap belsejének és a valós egyenesnek a Descartes-szorzata). Nagy gerjesztettség esetén a teljes
fázisoperátor koherens fázisállapotokon vett várható értéke a fűrészfog-függvényt közelíti, amely viselkedés
összhangban van az oszcillátor periodikus fázisváltozásáról alkotott klasszikus képpel.
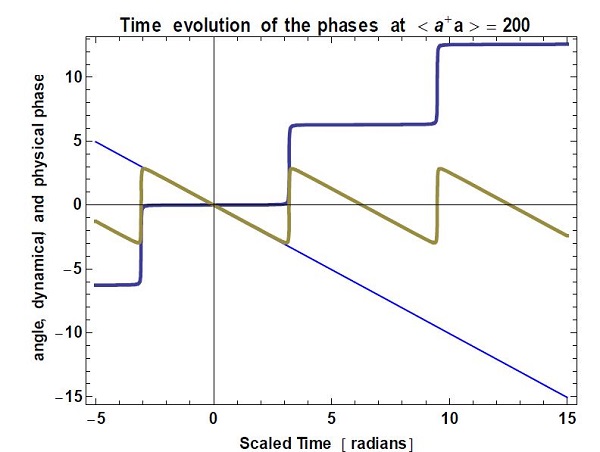
Figure 1. Shows the time evolution of the expectation value in a regular phase state (with mean photon number
200) of components of the regular phase operator (the reference phase has been taken -Pi). The straight line
with tangent -1 is the usual classical time dependence of a harmonic oscillator in phase space (clock-wise
rotation in the q-p plane), which has a sharp value, also for all quantum states of the oscillator. The
step-like curve (with 2Pi jumps) illustrates the gradual increase of the Blaschke contribution. The constant
values at the plateaus are exactly integer multiples of 2Pi, they are also sharp values for any oscillator
state. The 2Pi accumulations come from the invariant Haar integral of the positive operator-valued measure on
the Blasche group. The sum of these two contributions gives the periodic saw-tooth-like function, i.e. the
complete physical phase. For larger mean photon numbers this latter curve approaches the ideal saw-tooth
function.
References
[1] Varró S, Regular phase operator and SU(1,1) coherent states of the harmonic oscillator. Physica Scripta 90
(2015) 074053 (18pp) [Special Issue dedicated to the 150 years of Margarita and Vladimir Man’ko]. E-print:
arXiv:1412.3218v2.
[2] Varró S, Regular phase operator and a new number-phase Weyl-Wigner correspondence for the photon. Talk No.
53 at CEWQO-2015 [22nd Central European Workshop on Quantum Optics 6-10 July 2015, Warsaw, Poland]. Varró S,
Regular number-phase Wigner function of a photon mode. Invited talk S7.3.1. presented at Seminar 7: Quantum
information and quantum computation, of LPHYS’15 [24th International Laser Physics Workshop, 21-25 August
2015., Shanghai, P R China].
[3] Varró S, Regular phase operator of the photon as a Haar integral on the Blaschke group. Invited talk. 4th
Work Meeting on Quantum Optics & Information [Regional Centre of the Hungarian Academy of Sciences at Pécs,
6-7 May 2016., Pécs, Hungary]. Varró S, The quantum phase of the photon as a Haar integral on the Blaschke
group. Invited Talk S7.3.2 presented at Seminar 7: Quantum information and quantum computation, of LPHYS’16
[25th International Laser Physics Workshop, 11-15 July 2016., Yerevan, Armenia].
2016. szeptember 29. (csütörtök) 13:00
Előadó: Ayadi Viktor (MTA Wigner FK)
Cím: Koherencia és kvantum-klasszikus megfeleltetés ultragyors lézer-atom kölcsönhatásban
Kivonat |
Előadás
Atomi rendszerek lézerimpulzusokkal történő kölcsönhatása esetén a magasrendű harmonikuskeltés (HHG) és a
küszöbfeletti ionizáció (ATI) jól ismert jelenségek. Ezek elméleti és kísérleti vizsgálatát mindezidáig (a
folyamat kezdetén) alapállapotban lévő atomokra korlátozták. Viszont új izgalmas effektusok lépnek fel, ha
szuperpozíciós kezdőállapotot feltételezünk (pl.: 2s-3p), ugyanis kimutattam, hogy lézerterekkel kölcsönható
atomi szuperpozíciós állapotok erős koherenciajelenségeket mutatnak [1]. Megfigyeltem, hogy az állapotok közti
relatív fázis alkalmas megváltoztatása akár háromszorosára is emelheti az ionizációs valószínűséget. A
kérdéskör tanulmányozásának legfőbb eszközéül az időfüggő Schördinger egyenlet (TDSE) numerikus integrálása
szolgált.
A másik munkámban a hidrogénatom alapállapoti fotoionizációja során emittált elektronok impulzuseloszlását
vizsgáltam egy szemiklasszikus Monte Carlo módszerrel (SCMC), melynek eredményei jó egyezést mutatnak a
kvantummechanikai modellel [2]. Megvizsgáltam, hogy az eloszlás különböző interferencia maximumaihoz milyen
tipikus kezdőfeltételű elektronpályák tartoznak az SCMC módszer által nyújtott klasszikus képben. A
szemléletes kvantum-klasszikus megfeleltetésen túl nagy előnye még az SCMC módszernek, hogy viszonylag könnyen
átvihető nem-triviális geometriájú rendszerekre is.
A TDSE és SCMC módszerek vizsgálata és megfeleltetésük (a fenti alapkutatási felfedezéseken túl) megfelelő
előtanulmányt jelentett plazmonikus nanostruktúrákról történő fotoemisszió [3] kvantummechanikai
modellezéséhez is, amely jelenlegi kutatásaim fókuszát jelentik.
Referenciák:
[1] V. Ayadi, M. G. Benedict, P. Dombi, P. Földi, Atomic coherence effects in few-cycle pulse induced
ionization, Europen Physics Journal D, bírálat alatt, arXiv: 1604.03437 (2016).
[2] V. Ayadi, P. Földi, P. Dombi, K. Tőkési, Correlations between the final momenta of electrons and their
initial phase-space distribution in the process of tunnel ionization, Journal of Physics B, bírálat alatt,
arXiv: 1604.04507 (2016).
[3] I. Márton, V. Ayadi, P. Rácz, T. Stefaniuk, P. Wróbel, P. Földi, P. Dombi, Ultrafast Plasmonic Electron
Emission from Ag Nanolayers with Different Roughness, Plasmonics, nyomdában (2016).
2016. szeptember 22. (csütörtök) 13:00
Előadó: Érdi Bálint (ELTE, Csillagászati Tanszék)
Cím: A sárkánykonfigurációk
Egy megoldás csodái
Kivonat |
Előadás
A centrális konfigurációk nagy szerepet játszanak az n-test problémával kapcsolatos kutatásokban.
Centrális konfiguráció esetén az egyes testekre ható eredő erő mindig a rendszer tömegközéppontján megy
keresztül, és a testek önhasonló konfigurációjú mozgást végeznek. A háromtestprobléma centrális konfigurációi
az Euler-Lagrange-megoldások. n>3-ra a probléma megoldatlan, eddig csak részeredmények születtek. A
közelmúltban azonban sikerült a négytestprobléma egy tengelyszimmetrikus esetére olyan analitikus megoldást
találnunk, amely megadja a probléma összes megoldását.
Az előadás bemutatja a megoldáshoz vezető utat, a deltoid-alakú (sárkány) konfigurációk sokszínű világát, és
ezek kapcsolatát a Lagrange-megoldásokkal.
2016. szeptember 8. (csütörtök) 13:00
Előadó: Roósz Gergő (MTA Wigner FK)
Cím: Fluktuáló terű transzverz Ising-lánc
dinamikája
Kivonat |
Előadás
Az egydimenziós kvantum Ising modell dinamikáját vizsgálom zéró
hőmérsékleten, véletlenszerűen változó külső tér mellett.
Megmutatjuk hogy a modell dinamikája szoros kapcsolatban van egy
egydimeziós, folytonos idejű kvantumos bolyongással, amelynek az
átmeneti valószínűségei véletlenszerű időfüggéssel bírnak.
A külső zaj dekoherenciát okoz a rendszerben, a hullámcsomag
álltalában diffúzív módon szélesedik ki. Következményként a
kvantum Ising lánc átlagos összefonódási entrópiája t^{1/2}-el
arányosan nő, és az átlagos mágnesezettség logaritmusa is
hasonló jellegű viselkedést mutat.
Ha a külső zaj kétféle értéket vehet fel, és az értéke \tau
időközönként változhat meg, akkor bizonyos \tau értékeknél
létrejönnek koherens, ballisztikusan mozgó hullámcsomagok, aminek
következtében az összefonódási entrópia és az átlagos
mágnesezettség logaritmusa is t^{3/4}-es viselkedést mutat.
[G. Roósz, R. Juhász, F. Iglói Phys. Rev. B 93, 134305 (2016)]
2016. április 14. (csütörtök) 13:00
Előadó: Majorosi Szilárd (SzTE, Elm. Fiz. Tansz.)
Cím: Időfüggő Schrödinger-egyenlet pontos numerikus megoldása szinguláris Coulomb potenciál esetén
Kivonat
Az attoszekundumos fizikában, különösen a pumpa-próba kísérletek eredményeinek értelmezéséhez, elengedhetetlen
az alagutazásos ionizáció dinamikájának pontos elméleti ismerete. A probléma természetéből adódóan, ehhez
pontos numerikus szimulációkra is szükség van. Az előadás keretében bemutatunk egy újszerű és hatékony
numerikus algoritmust a 3D forgásszimmetrikus időfüggő Schrödinger-egyenlet megoldására, amely szinguláris
Coulomb potenciált is tartalmaz. A problémát hengerkoordinátákban tárgyaljuk és formalizmusunk kimondottan
alkalmas lézer-atom kölcsönhatás tárgyalására (dipólközelítéssel és ún. hossz-mértékben). Negyedrendű véges
differencia közelítést használunk valós térkoordinátákban, és a Coulomb szingularitásokat a megfelelő Neumann
és Robin peremfeltételek diszkretizációjával kezeljük. Időfejlesztő algoritmusunk a Crank-Nicolson és a
split-operator módszereket használja, amelyet továbbfeljesztettünk negyedrendű időlépésbeli pontosságot is
elérve. Alkalmazásként intenzív lézertér hatására alagutazásos ionizációval kiszabaduló atomi elektron
dinamikáját elemezzük.
2016. április 7. (csütörtök) 13:00
Előadó: Barna Imre Ferenc (MTA Wigner FK)
Cím: Nemlineáris parciális differenciálegyenletek önhasonló analízise
Kivonat
Előadásom során bemutatom az önhasonló Ansatz-ot amelynek használata egy erős
és célravezető módszer gyakorlatilag mindenféle nem-lineáris parciális differenciálegyenlet
analízisében. Az Ansatz teljesítőképességét egy áramlástani és egy nemlineáris
elektrodinamikai példán mutatom meg.
2016. március 3. (csütörtök) 13:00
Előadó: Juhász Róbert (MTA Wigner FK)
Cím: Hosszú hatótávolságú, rendezetlen rendszerek kritikus viselkedése
Kivonat |
Előadás
A hosszú hatótávolságú (azaz a távolság negatív hatványával csökkenő erősségű) kölcsönhatást feltételező
sokrészecske-rendszerek fázisátalakulási jellemzői eltérőek lehetnek a rövid hatótávolságú rendszerekéitől.
Hasonlóan, a térbeli inhomogenitás (rendezetlenség) jelenléte is eltérést okozhat a homogén rendszerek
viselkedéséhez képest.
Az előadásban áttekintjük az inhomogén és hosszú hatótávolságú spinmodellek fázisátalakulásainak
jellegzetességeit. Ezt követően, ezen két tényező együttes hatását vizsgáljuk meg egy konkrét modell, a
merőleges terű Ising-modell alapállapotában. Ismertetünk egy közelítő, valós-tér renormálási sémát,
amely az egydimenziós modell paramágneses fázisában és kritikus pontjában alkalmazható. Az eredmények szerint
a paramágneses fázisban Griffiths-effektus lép fel, a kritikus ponti viselkedést pedig egy végesen rendezetlen
fixpont írja le. Egy – ugyanebbe az univerzalitási osztályba tartozó – járványterjedési modell, a hosszú
hatótávolságú, rendezetlen kontakt-folyamat Monte Carlo szimulációja az elméleti eredményekkel
összhangban álló viselkedést mutat.
2016. február 18. (csütörtök) 13:00
Előadó: Katz Sándor (ELTE, Elméleti Fizikai Tanszék)
Cím: A tömeg eredete a látható világegyetemben
Kivonat |
Előadás
Az utóbbi évek egyik legnagyobb tudományos eredménye a Higgs bozon felfedezése volt. A Higgs felelős az elemi
részecskék tömegéért. A
látható világegyetem tömegét azonban szinte kizárólag protonok és neutronok adják, melyek nem elemi
részecskék. Ezek tömegének eredete
jóval összetettebb, a Higgs csak egy kis részükért felelős. A részecskefizika standard modelljét alkotó három
kölcsönhatás mindegyike
hozzájárul a tömeghez. Az előadás áttekinti ezeket a járulékokat, összehasonlítja nagyságukat és bemutatja az
erre vonatkozó legújabb
tudományos eredményt: a neutron és proton tömegkülönbségének elméleti meghatározását.
2016. február 4. (csütörtök) 13:00
Előadó: Mati Péter (ELI ALPS)
Cím: Soft photon resummation in QED and the Bloch Nordsieck model
Kivonat |
Előadás
Infrared (IR) singularities in massless gauge theories are known since the foundation of quantum field
theories. The root of this problem can be tracked back to the very definition of these long-range interacting
theories such as QED.
We will briefly review the basics of QED: Lagrangian formalism, Feynman rules, etc...
The IR catastrophe and its resolution by cancelling these divergences will be also discussed. The
Bloch-Nordsieck model provides the IR limit of QED and in its framework all the radiative corrections to the
electron propagator can be fully summed. However, perturbation theory does not provide the right tool for this
operation: the exact Dyson-Schwinger (DS) equation needed to be solved with the aid of the Ward-Takahashi
identities. Solving the DS equation at finite temperatures is also possible and will be presented in the talk.
Szemináriumok 2015-ben
2015. december 17. (csütörtök) 13:00
Előadó: Szabó Lóránt Zsolt (SZTE Elm. Fiz. Tansz.)
Cím: Időfüggő kvantumos szórási folyamatok
Kivonat |
Előadás
Az időben oszcilláló külső potenciálok sok esetben szolgáltatják a lézertér jó modelljét. Periodikusan változó
potenciális energia esetén matematikailag a Floquet-elmélet jelent hatékony módszert a különböző időfüggő
kvantumos szórási folyamatok leírásához.
Az előadásom során egy relativisztikus és egy nemrelativisztikus modellt fogok bemutatni. Modelljeinkben
monoenergiás elektronhullámot tekintünk, amely az egyik esetben oszcilláló potenciálgáton szóródik [1], a
másikban pedig kölcsönhat egy "kemény gömb"-bel, ahol a folyamat időfüggését intenzív lézertér jelenléte adja
[2].
[1] L. Zs. Szabó, M. G. Benedict, A. Czirják and P. Földi, Phys. Rev. B 88, 075438 (2013); DOI:
10.1103/PhysRevB.88.075438
[2] S. Varró, L. Zs. Szabó and A. Czirják, Nucl. Instr. Meth. B. (2015) (in press); DOI:
10.1016/j.nimb.2015.10.064
2015. december 3. (csütörtök) 13:00
Előadó: Lukács Árpád (MTA Wigner FK, RMI, Budapest)
Cím: Síkhullám mint vonósugár
Kivonat |
Előadás
Megmutatjuk, hogy szórási problémák egy tág osztályában a beeső síkhullám vonósugárként viselkedik, azaz, a
szokásos sugárzási nyomás jelenségétől eltérően nem ellöki, hanem vonzó erőt fejt ki a szórócentrumra. A
jelenség
magyarázata, hogy a beeső hullám átalakul egy másik csatornában kifutó,
nagyobb imulzussűrűségű hullámmá, ilymódon a szórócentrum mögött
imulzustöbblet alakul ki a hullámtérben. Ez a vonsósugár vagy negatív
sugárzási nyomás többcsatornás szórás esetén generikus. A jelenséget példákkal
illusztrálom: kettőstörő közegben terjedő elektromágneses hullámok vékony,
szintén kettőstörő lapon való áthaladásakor is fellép a jelenség, és
mesterséges dielektrikumok esetében akár makroszkopikus is lehet. További
példákat szolgáltat a lassú neutronok szóródása az XY modellel leírt anyag
mágneses vortexein, vagy nehéz barionok könnyű leptonokká való konverziója
kozmikus húrokon való szóródás során.
Az előadás anyagát képező cikk:
Forgács, Lukács, Romanczukiewicz, Phys Rev D88, 125007 (2013).
2015. november 12. (csütörtök) 13:00
Előadó: Csörgő Tamás (MTA Wigner FK, Budapest és KRF, Gyöngyös)
Cím: Kvantum-optikai módszerek a nagyenergiás részecske- és magfizikában
Kivonat |
Előadás
Előadásomban a kvantum-optika nagyenergiás fizikai alkalmazásainak néhány érdekességét mutatom be, különös
tekintettel a femtométeres hosszskálán és a femtométer/c időskálán történő távolság és időmérések módszertani
hátterére. Felvillantom a Glauber-féle többszörös diffraktív szóráselmélet alkalmazásait, a Hanbury Brown -
Twiss effektuson alapuló femtoszkópiai mérések érdekességeit és bemutatok egy új, általunk kifejlesztett
modell-független korrelációs analízis módszert is, amelynek lehetséges alkalmazási területei jóval
túlmutathatnak a részecske- és magfizikán.
Hivatkozások:
F. Nemes, T. Csörgő, M. Csanád, http://arxiv.org/abs/1505.01415.
T. Csörgő, R. J. Glauber, F. Nemes, http://arxiv.org/abs/1311.2308.
T. Csörgő, T. Novák, H.C. Eggers and M. de Kock, http://arxiv.org/abs/1206.1680.
és előkészületben lévő, konferenciákon már bemutatott eredmények
2015. október 29. (csütörtök) 13:00
Előadó: Mikóczi Balázs (Wigner FK, Budapest)
Cím: Forgó testek mozgása az általános relativitáselméletben
Kivonat | Előadás
Az előadásomban áttekintésre kerül a forgó testek mozgásának leírása az általános
relativitáselméletben. Ismert, hogy a forgó próba részecskére vonatkozó Mathisson-Papapetrou egyenletek nem
zártak, így szükség van
valamilyen ún. spin koordináta feltétel választásra (spin supplementary condition, a továbbiakban SSC). Az
SSC-kből az irodalomban 4-féle létezik,
melyek közül 2 ekvivalens a (spinben lineáris) spin-pálya kölcsönhatásra.
A továbbiakban a kompakt forgó kettősre vonatkozó gyorsulásfüggő
Lagrange-formalizmus kerül tárgyalásra. Példákon keresztül bemutatásra kerül az általánosított
Lagrange-függvény kezelhetősége, illetve az ún.
Ostrogradsky-féle hamiltoni mechanika, az egyes SSC-kre. Végül tárgyalni
fogom a kettősre vonatkozó mozgásállandók, illetve a gravitációs sugárzás
által a megfigyelhető mennyiségek közül melyek függenek az SSC-ktől.
2015. október 15. (csütörtök) 13:00
Előadó: Gyenge Ádám (Rényi Intézet, Budapest)
Cím: Cayley-októniók és a G2 Lie-csoport
Kivonat |
Előadás
Folytatható-e a következő
sorozat: valós számok, komplex
számok, kvaterniók? Bár a kvaterniók már csak ferdetestet alkotnak, a
válasz a kérdésre mégis igen. A következő lépés, a Cayley féle
októniók, amik egy nem kommutatív divizióalgebrát alkotnak. Egy másik
érdekes kérdés, hogy mi ezen algebrák automorfizmus csoportja.
Előadásomban bemutatom az októniókat is előállító általános
konstrukciót, továbbá megvizsgáljuk az októniók automorfizmus
csoportját, a G2 Lie csoportot, illetve annak topológiáját is. Az idő
függvényében a G2 csoport egy másik nézőpontját is bemutatom,
amely a bizonyos fizikai elméletekben jelentős G2 sokaságok
definíciójához vezet.
2015. szeptember 17. (csütörtök) 13:00
Előadó: Néda
Zoltán (Babeş-Bolyai Tudomanyegyetem, Fizika Kar)
Cím: Kinetikus érdesedés egy visszahúzódó folyadékhártya
peremén
Kivonat
Egy elegáns számítógép
szimulációs módszert mutatunk be, amely jól használható felületeken
elkent vékony és viszkózus folyadékrétegek visszahúzódási dinamikájának
tanulmányozására [1]. Módszerünk egy molekuláris dinamika tipusú
megközelítés, melyben a folyadék hármasvonala (felület-levegő-folyadék
találkozási tartománya) diszkretizált, és a diszkretizálást meghatározó
karakterisztikus pontok mozgásegyenleteit integráljuk (1. Ábra). A
módszer hatékonyságát és alkalmazhatóságát egy inhomogén felületre
alkalmazott tüzőerőkkel müködő modellen keresztül mutatjuk be [2,3].
Modellünk kétparaméteres állapotterében feltérképezzük a hármasvonal
dinamkáját és topologiáját jellemző rendparamétereket. Modellünkben és
szimulációs módszerünkben megengedjük a felület felszakadását, szigetek
kialkulását és a hármasvonal komplex összeesését. Újfajta kinetikus
fázisátalakulás jelenlétére [4,5] utaló eredményeket mutatunk be,
melynek eredményeképp nemtriviális kollektív viselkedés tapasztalható
bizonyos paraméter tartományban. Ezen tartományban levő kritikus
érdesedés a felületi inhomogenitás és a kapilláris erők versengésének
tulajdonítható.
1. Ábra: A
folyadék hármasvonalának a diszkretizálása és a molekuláris dinamika
megközelítés alapötlete.
Kulcsszavak: felületi nedvesítés,
molekuláris dinamika szimuláció, dinamikus fázisátalakulás, kritikus
viselkedés
Bibliográfia:
[1] B. Tyukodi, Y. Brechet, Z. Neda, Phys. Rev. E, 90, 052404 (2014)
[2] P. G. Gennes; Rev. Mod. Phys. 57, 827 (1985)
[3] J.F Joanny, P. G. de Gennes; J. Chem. Phys. 81, 552 (1984)
[4] A. Tanguy, M. Gounelle, S. Roux; Phys. Rev. E 58, 1577 (1998)
[5] S. Krishnamurthy, A. Tanguy, S. Roux; Eur. Phys. J. B 15, 149
(2000)
2015. szeptember 3. (csütörtök) 13:00
Előadó: Balog János (Wigner FK, RMI)
Cím: Y és T rendszerek rács Wess-Zumino-Witten
reprezentációja
Kivonat
Az Y és T rendszerek
érdekes differencia egyenletek, amelyek az elméleti fizika számos
területén megjelennek. Ezek között vannak rács statisztikus modellek,
az integrálható modellek termodinamikáját leíró TBA egyenletek és
újabban az AdS/CFT korrespondencia spektrális problémája. Megmutatjuk,
hogy ezen rendszereket klasszikus rács Wess-Zumino-Witten modellekként
is lehet interpretálni. Ez az interpretáció hasznosnak bizonyul ezen
rendszerek vizsgálatában, például periodicitási tulajdonságuk
bizonyításánál.
2015. május 27. (szerda) 15:00
Előadó: I.
Marshall (Faculty of Mathematics, HSE, Moscow)
Cím: A new model in the Calogero-Ruijsenaars family
Kivonat (angolul)
After presenting a brief
summary of the mathematical background, I explain how Hamiltonian
reduction can be used to project a trivially integrable system on the
Heisenberg double of SU(n,n), to obtain a system of Ruijsenaars type on
a suitable quotient space. This system possesses BC(n) symmetry and is
shown to be equivalent to the standard three-parameter BC(n) hyperbolic
Sutherland model in the cotangent bundle limit.
2015. május 14. (csütörtök) 13:00
Előadó:
Kónya Gábor
(Wigner FK, SZFI)
Cím: Egy optikai rezonátorba helyezett Bose-Einstein
kondenzátum polariton lágy módusának bomlása
2015. május 7. (csütörtök) 13:00
Előadó: L.D.
Faddeev (St. Petersburg Dept. of Steklov Math. Inst.)
Cím: The new life of integrability
Kivonat (angolul) | Előadás
The notion of complete
integrability stems from the formalism of Hamiltonian mechanics of the
XIX century and the search for concrete examples was a kind of exotic
sport. The situation changed drastically in the second half of the last
century, when realistic examples of completely integrable infinite
dimensional Hamiltonian systems were constructed. The first example of
the Korteveg-de Vries equation was followed by many other systems with
natural quantization. Spin chains gave another line of development.
This culminated in the formulation of a general theory of integrable
systems, based on the Yang-Baxter equation and Bethe Ansatz. New
applications in recent times appeared in relativistic quantum field
theory. I shall give an elementary survey of this development.
2015. április 23. (csütörtök) 14:00
Előadó:
Bucz Gábor
(SZTE, Elméleti Fizikai Tanszék, PhD hallgató)
Cím: Kevert állapoti anholonómiák vizsgálata
Kivonat |
Előadás
A kvantum
információelmélet és a kvantum-összefonódás vizsgálata mai napig nagy
kihívást jelent az elméleti fizikusok számára. A kevert állapoti
anholonómiák vizsgálata során alkalmazott matematikai módszerek
hasonlóak kvantum információelmélet és a kvantumos összefonódás
leírásánál használtakkal, így a kevert állapoti geometriai fázis
fizikájának és matematikájának megértése lehetőséget ad a témák közötti
átfedés feltérképezésére. Megvizsgáljuk, hogy a nyalábstruktúra, mint
absztrakt matematikai elgondolás hogyan fordul elő kvantummechanikai
problémákban. A fizikusok által jól ismert Berry fázis egy
általánosítását összehasonlítottuk a kevert állapotokon definiált
fázissal, amelyek, mint kiderült, egymással egyenértékűek megfelelő
megszorítással. Jelenleg is folyik a munka afelé, hogy a két qubit
összefonódást magasabb dimenziós rendszerekbe beágyazzuk. Reményeink
szerint a beágyazás által a két részrendszerre vonatkozó egyenletek
ebben az esetben egy egyszerűbb formalizmusra vezetnek, ezáltal
közelebb kerülhetünk a probléma mélyebb megértéséhez.
2015. március 26. (csütörtök) 13:00
Előadó: Rácz
István (Wigner FK, RMI)
Cím: Szabadsági fokok az Einstein-féle gravitációelméletben
Kivonat |
Előadás
Az elmúlt évben az
Einstein-féle gravitációelmélet dinamikai szabadsági fokainak egy új,
geometriailag kitüntetett ábrázolását vezettük be. Ezzel párhuzamosan
egy olyan módszert dolgoztunk ki, amely lehetővé teszi a megoldások
szignatúrától független szimultán vizsgálhatóságát. Ezeket alkalmazva
az előadásomban először az Einstein-egyenletek különféle
alrendszereinek belső kapcsolataira mutatunk rá, melyek alapvető
fontossággal bírnak az evolúciós probléma megoldása során. Ezt követően
a kezdőadatok kiválasztásban főszerepet játszó kényszeregyenletek
kauzális jellegét érintő meglepő lehetőségre mutatunk rá.
2015. március 19. (csütörtök) 13:00
Előadó: Zaránd
Gergely (BME, Elméleti Fizika Tanszék)
Cím: Mott skyrmionok, avagy hogyan stabilizálhatunk
topológiai gerjesztéseket erős kölcsönhatással
Kivonat (angolul) | Előadás
Topological excitations
keep fascinating physicists since many decades. While individual
vortices and solitons emerge and have been observed in many areas of
physics, their most intriguing higher dimensional topological
relatives, skyrmions and magnetic monopoles remained mostly elusive. We
propose that loading a three-component nematic superfluid such as 23Na
into a deep optical lattice and thereby creating an insulating core,
one can create topologically stable skyrmion textures and investigate
their properties in detail. We show furthermore that the spectrum of
the excitations of the superfluid and their quantum numbers change
dramatically in the presence of the skyrmion, and they reflect the
presence of a trapped monopole, as imposed by the skyrmion's topology.
Signatures of the presence of the skyrmion in time of flight
experiments as well as experimental protocols to create it will also be
discussed [M. Kanász-Nagy, B. Dóra, E. A. Demler, and G. Zaránd,
Scientific Reports 5, 7692 (2015)].
2015. március 12. (csütörtök) 13:00
Előadó: Pályi
András (ELTE, Anyagfizikai Tanszék)
Cím: Pauli-blokád szén nanocsövekben
Kivonat
Mezoszkopikus
szilárdtestfizikai rendszerekben számos rendhagyó elektromos
transzportjelenség figyelhető meg. Egy példa az ún. Pauli-blokád: ha
egy kettős kvantumdoton áramot akarunk átfolyatni, akkor bizonyos
esetekben a töltések áthaladását meghiúsítják a Pauli-elv miatt fellépő
kiválasztási szabályok. Az előadásban bemutatom a Pauli-blokádra
vonatkozó első kísérleteket, az azokat leíró egyszerű modellt, és azt
hogy a jelenség hogyan alkalmazható elektronspin-alapú kvantumbitek
inicializálására és kiolvasására. Bemutatok egy Pauli-blokád
kísérletet, ahol szén nanocsőben vizsgálták a jelenséget, és
összehasonlítom a mért adatokat a saját elméleti eredményeinkkel. Az
eredmények szerint a nanocsövön átfolyó áram jelentősen megváltozhat a
külső mágneses tér kis változására. Ez elvileg módot ad arra hogy ezt a
nanoszerkezetet finom térbeli felbontású és érzékeny
mágnesestér-szenzorként használják, például egy inhomogén mágneses tér
pásztázószondás feltérképezésére. Bemutatom ennek a javasolt eljárásnak
a működési elvét, előnyeit és korlátait.
2015. február 26. (csütörtök) 13:00
Előadó: Dömötör
Piroska (SZTE, Elméleti Fizikai Tanszék)
Cím: Forgó molekulák áthaladása apertúrán: egy egyszerű
kvantummechanikai modell
Kivonat |
Előadás
Az előadásban egy
leegyszerűsített kétdimenziós forgó molekula modellt vizsgálunk. A
tömegközéppont csak az apertúra szimmetriatengelye mentén mozoghat így
a rés nem-triviális módon összefonja a transzlációs és a rotációs
szabadsági fokot. A geometriai modell bonyolult peremfeltételű
akadályon való két dimenziós kvantumos szórási problémára vezet. A
stacionárius szórási problémát először közelítéseket alkalmazva
analitikusan vizsgáljuk. Azután az analitikus eredmények ellenőrzésére
a probléma Green-függvényének meghatározásán alapuló, numerikusan
egzakt megoldást keresünk. Célunk nagy élettartamú rezonáns állapotok
beazonosítása és a transzmissziós valószínűség energiafüggésének
meghatározása.
2015. február 12. (csütörtök) 13:00
Előadó: Bajnok
Zoltán (Wigner FK, RMI)
Cím: A mérték/gravitáció dualitás
Kivonat |
Előadás
Világunk négy alapvető
kölcsönhatásának (erős, gyenge, elektromágneses és gravitációs) a
relativitáselmélettel összhangban lévő kvantumos leírása csak
részecskék kicserélődésével valósítható meg. Az elektromágneses
kölcsönhatás során pl. fotonok, az erős esetén gluonok cserélődnek ki.
De amíg a több fotonos folyamatok járuléka egyre kisebb, addig a több
gluoncseréseké egyre nagyobb, lehetetlenné téve az erős folyamatok
pontos számítását. A gravitációs kölcsönhatásnak máig sincs elfogadható
kvantumos leírása. A mérték-húr dualitás egyszerre ad reményt a
kvantumgravitáció megértésére és az erősen csatolt mértékelméletek
dinamikájának leírására, hiszen a gravitációt is tartalmazó
húrelméletet mértékelméleteknek felelteti meg. A megfeleltetés
holografikus abban az értelemben, hogy a húrok anti de Sitter téren
történő mozgása ekvivalens az anti de Sitter tér négydimenziós peremén
létrejövő árnyékuk színes mértékkölcsönhatásával. A dualitás egy
sejtés, mely az erősen kölcsönható mértékelméleteket klasszikus
gravitációra, míg kvantumos húrelméletet perturbatív mértékelméletre
képzi le. Előadásomban motiválom a holografikus sejtést, áttekintem az
alátámasztására tett hatalmas erőfeszítéseket és összefoglalom a
kutatás legújabb fejleményeit.
Szemináriumok 2014-ben
2014. december 18. csütörtök du. 13:00
Előadó: Varró
Sándor (Wigner FK, SZFI)
Cím: Haar Alfréd fizikai matematikája. I-II. (folytatás)
Kivonat |
Előadás
Haar Alfréd (1885–1933) a
múlt század első felében – Riesz Frigyes mellett – a matematika
legjelentősebb, nemzetközi hírű magyarországi képviselője volt.
Harmincöt publikációjában [1] megjelent számos eredménye az elméleti
fizikában is fontos szerepet játszik. Erre példaként említhetők a
Sturm–Liouville-féle differenciálegyenletekhez kapcsolódó ortogonális
függvényrendszerekre vonatkozó tételei [2a-b-c], amelyek a
Schrödinger-féle hullámmechanika konkrét felhasználásának alapját
képezik.
Előadásunkban kiemeljük a
Haar-féle ortogonális függvényrendszert (Haar-wavelet,1909) [2], a
több-dimenziós variációszámításban elért eredményeket (Haar-lemma,1922)
[3], valamint az invariáns mérték megkonstruálását lokálisan kompakt
topológikus csoportokon (Haar-mérték, 1932) [4]. Ez utóbbi eredmény
döntő jelentőségű volt a Hilbert-féle ötödik probléma (1900)
megoldásában. Időközben a Haar-mérték az absztrakt harmonikus analízis
nélkülözhetetlen eszközévé vált [5], és alkalmazást nyert a
kvantumelméletben is [6]. Megemlítjük még, hogy Haar a lineáris
egyenlőtlenség-rendszerekre vonatkozó Farkas-féle tételt (1901)
általánosította inhomogén rendszerekre [7], s mint az ma már jól
ismert, Farkas Gyula idevágó eredményei a modern optimalizáláselmélet
kialakulásában alapvető szerepet játszottak [8]. Megkíséreljük e
korszakalkotó eredmények hatását és utóéletét érzékeltetni. Elsősorban
a Haar-wavelet korai történetével és továbbfejlesztéséseivel
foglalkozunk, amelyek az 1980-as évektől a jelanalízisben [9] és az
információfeldolgozásban (pl. JPEG tömörítés) fontos szerepet kaptak.
Riesz 1911-ben, Haar
1912-ben kifejezetten Farkas Gyula közbenjárására került a kolozsvári
egyetemre: „Ime Riesz Frigyes társunk már javában megkezdte itteni
működését nagy lelkesedéssel a math. szeminárium körül is. ... Tegnap
levelet kaptam Haartól. ... Egyébiránt Haar levele oly mély hazafias
érzelmeket árul el, hogy mostmár nem is tartok attól, hogy ha egyszer
haza kerül, elveszítjük a külföldnek. ...” [8]. Haar Alfrédnak a múlt
századi magyar oktatás és tudományos közélet érdekében kifejtett
tevékenysége is múlhatatlan jelentőségű. „Az első világháború után
Erdélynek Magyarországtól való elcsatolása következtében az addigi
kolozsvári egyetem tanárainak el kellett hagyniok e várost és előbb
átmenetileg Budapesten, majd 1920-tól Szegeden folytatták működésüket.
Haar Alfréd és Riesz Frigyes az új szegedi matematikai szemináriumot –
amelyet később Bolyai Intézetnek neveztek el – hamarosan nemzetközi
tekintélyű matematikai centrummá fejlesztették. … Egyetemi előadásainak
tárgyát Haar leginkább az algebra számelmélet, analitikus geometria,
mechanika, differenciálegyenletek, variációszámítás, folytonos
csoportok elmélete területeiről választotta. Elsőrangú egyetemi előadó
volt, előadásai világosságban, logikus felépítésben mintaszerűek
voltak. …” Haar Alfrédtől könyv nem jelent meg. Azonban több igen
gondosan megírt jegyzetet készített.... Noha ezek az egyetemi előadások
sok eredeti részletet tartalmaznak, s mint egyetemi tankönyvek ma is
beválnának, a jelen összegyűjtött munkák közé való felvételükről már
csak terjedelmük miatt sem lehetett szó.” (Szőkefalvi-Nagy Béla,
Bevezetés, Haar Alfréd rövid életrajza [1]). Előadásunkban e nem
publikált egyetemi jegyzetekből is mutatunk be (tudomásunk szerint a
szélesebb tudományos közönség számára mindezidáig ismeretlen)
szemelvényeket.
Irodalom
[1] Haar A, Összegyűjtött Munkái. Sajtó alá rendezte Szőkefalvi-Nagy
Béla (Akadémia Kiadó, Budapest, 1959).
[2a] Haar A, Zur Theorie der orthogonalen Funktionensyteme ( Inaugural
Dissertation zur Erlangung der Doktorwürde der hohen
philosophischen Fakultät der Georg-August-Universität zu Göttingen,
vorgelegt von Alfred Haar aus Budapest). 1909, 1-49.
[2b] Haar A, Zur Theorie der orthogonalen Funktionensyteme (Erste
Mitteilung). Mathematische Annalen 69,
331-371 (1910).
[2c] Haar A, Zweite Mitteilung; ibid. 71,
38-53 (1911)
[3a] Haar A, Über die Variation der Doppelintegrale. Journal
für reine und angewandte Math. 149, 1-18
(1919).
[3b] Haar A, Über eine Verallgemeinerung de Du Bois-Reymond’schen
Lemmas. Acta Sci. Mathematicarum Szeged 1,
33-38 (1922).
[3c] Haar A, Über das Plateausche Problem. Math. Ann.
97, 127-158 (1926)
[4a] Haar A, Székfoglaló értekezés a Magyar Tudományos Akadémián (1932.
Április 18): A folytonos csoportok elméletéről. Mathematikai
és Természettudományi Értesítő, Budapest 49,
287-307 (1932).
[4b] Haar A, Der Maßbegriff in der Theorie der Kontinuierlichen
Gruppen. Annals of Mathematics (2) 34,
147-169 (1933)
[5a] Hewitt E and Ross K A, Abstract Harmonic Analysis I
(Vol. I: Structure of Topological Groups, Integration Theory, Group
Representations) (Springer-Verlag, New York, Inc., 1963, 1979).
[5b] Hewitt E and Ross K A, Abstract Harmonic Analysis II
(Vol. II: Structure and Analysis for Compact Groups, Analysis on
Locally Compact Abelian Groups) (Springer-Verlag, Berlin, Heidelberg,
1970)
[6] Mackey G W, The significance of invariant measures for harmonic
analysis. Colloquia Mathematica Societatis János Bolyai, 49., Budapest,
Hungary, 1985. In Szabados J and Tandori K (editors), Alfréd
Haar Memorial Conference Vol. II. (North-Holland Publishing
Company, Amsterdam, 1987) pp. 551-608.
[7] Haar A, A lineáris egyenlőtlenségekről. Mathematikai és
Természettudományi Értesítő, Budapest 36,
279-296 (1918). Über lineare Ungleichungen. Acta Scientiarum
Mathematicarum Szeged 2, 1-14 (1924).
[8] Prékopa András, Farkas Gyula élete és munkásságának jelentősége az
optimalizálás elméletében. In Martinás Katalin (Szerk.), Farkas
Gyula élete és munkássága. (ELFT Termodinamikai Szakcsoport,
Budapest, 2003) pp 9-26.
[9] Chui Charles K (Editor), WAVELETS : A Tutorial in Theory
and Applications. (Academic Press, Inc., Boston, San Diego,
1992)
2014. december 4. (csütörtök) 13:00
Előadó: Szaszkó-Bogár Viktor (SZTE, Elméleti Fizikai Tanszék)
Cím: Kvantumos transzportfolyamatok oszcilláló spin-pálya
kölcsönhatás jelenlétében
Kivonat |
Előadás
A mezoszkopikus rendszerek
a makro- és a mikrovilág hátárán elhelyezkedő objektumok. Ebbe a
családba tartoznak a nanostruktúrák, melyek elektromos és mágneses
tulajdonságait a kvantumos interferencia jelenségek határozzák meg.
Kiemelkedő jelentőséggel bírnak a félvezető heterostruktúrák, melyekben
kétdimenziós elektrongáz jön létre, amely igen magas mozgékonysággal
rendelkező elektronokat tartalmaz.
Amennyiben a lézertérhez
hasonlóan, időben alternáló Rashba-féle spin-pálya csatolás van jelen a
nanorendszerben, akkor egy hatékony matematikai eszköztárat biztosít az
ún. Floquet-elmélet. Ezzel megmutatható, hogy az ilyen struktúrák
alkalmasak felharmonikus frekvenciák gerjesztésére.
A szeminárium keretében
azokat az eredményeket mutatom be, melyek az időfüggő spin-pálya
kölcsönhatás jelenlétében vizsgált transzportfolyamatok elméleti
vizsgálatai során születtek.
2014. november 27. (csütörtök) 13:00
Előadó: Paolo Casati (Università di Milano-Bicocca,
Department of Mathematics and its Applications)
Cím: The bi-Hamiltonian approach to integrable systems
Kivonat (angolul) | Előadás
The purpose of the talk is
to explain the basics of the bi-Hamiltonian theory of integrable
systems. After an introductory part devoted to presenting the main
concepts, we will describe two concrete examples. Our first example
will be the finite-dimensional Toda lattice. The second example is
infinite-dimensional, namely the celebrated Korteweg-de Vries equation.
This nonlinear partial differential equation played a pivotal role in
the whole theory. Both examples will illustrate how the bi-Hamiltonian
approach allows to construct a complete set of conserved quantities and
may be used to find solutions of the pertinent evolution equations.
2014. november 13. (csütörtök) 12:45
Előadó: Karsai
Márton (ENS de Lyon, Computer Science Department)
Cím: Online innovációk komplex terjedési folyamata
Kivonat
Az innovációk, termékek,
vagy alkalmazások terjedését értelmezhetjük diffúziós folyamatokként,
melyeket erősen befolyásolnak a szociális kölcsönhatások és a külső
média hatásai. Ezeknek a hatásoknak a jelenléte régóta elfogadott, de
jellemzésük és kísérleti megerősítésük mindmáig váratott magára
megfelelő adatok hiányában. Munkánk során célunk a kérdéses folyamatok
megértése és modellezése volt, az egyik legnagyobb elérhető adathalmaz,
a Skype szociális hálózatának és terjedésének elemzésével. Sikerült
bizonyítanunk korábbi feltételezéseket, miszerint a szociális terjedési
folyamatok leírhatóak konstans terjedési rátákkal és olyan lineárisan
növekvő szociális nyomással, ami az egyén közvetlen környezetéből
érkezik. A megfigyelt mechanizmusokat egy dinamikus diffúziós modellben
egyesítettük, ami alkalmasnak bizonyult arra, hogy előre jelezze
középtávon az online alkalmazás terjedését különböző országokban, és
rámutatott arra, hogyan függ össze a terjedés dinamikája és az adott
ország gazdasági fejlettsége.
2014. október 30. (csütörtök) 13:00
Előadó: Gehér
György Pál (SZTE, Bolyai Intézet)
Cím: Wigner tétele kvantummechanikai szimmetriákról
Kivonat |
Előadás
1932-ben Wigner állította,
hogy a tiszta állapotok egy olyan bijektív transzformációja, mely
megőrzi az átmenetvalószínűségeket, mindig egy unitér vagy egy
antiunitér operátor által megvalósított leképezés. Ennek a tételnek az
első igazán precíz bizonyításait 1962-ben U. Uhlhorn, 1963-ban J. A.
Lomont és P. Mendelson, illetve 1964-ben V. Bargmann adták, egymástól
függetlenül. Ezek a bizonyítások ugyan követhetőek, de eléggé nehezen.
Azóta rengeteg bizonyítás született Wigner tételére, s annak
nem-bijektív verziójára is, illetve sok irányban általánosították ezt a
híres, kvantummechanikában igen fontos tételt. Az első kristálytiszta
bizonyítás egy magyar matematikus, Molnár Lajos nevéhez fűződik,
1996-ból. Ugyanakkor a bizonyítás erős matematikai tételeket használ
fel, tehát ilyen értelemben nem mondható eleminek.
Az előadáson részletesen
szeretnék ismertetni egy abszolút elemi (csupán alap Hilbert térbeli
fogalmakat használó), és nagyon rövid bizonyítást, mely a Wigner tétel
legáltalánosabb verziójára megy (nem tesszük fel a bijektivitást, és a
Hilbert tér dimenziójáról sem teszünk fel semmit). Minden szükséges
definíciót ismertetni fogok. Ez a bizonyítás 2014 februárjában
született, és egy fogalom, az úgynevezett "metrikus rezolvens halmaz"
inspirálta.
Ha marad idő, szeretnék
kitérni a bijektív Wigner tétel Uhlhorn féle általánosítására is,
illetve a projektív geometria alaptételére, mellyel tulajdonképpen be
lehet látni az Uhlhorn tételt. Az Uhlhorn és Wigner tételek egyéb
általánosítási lehetőségeiről is szót szeretnék ejteni.
2014. október 16. (csütörtök) 13:00
Előadó: Asbóth
János (Wigner FK, SZFI)
Cím: Topologikusan védett élállapotok egy periodikusan
gerjesztett, királisan szimmetrikus kvantumdróton
Kivonat
A kvantummechanika egyik
korai diadala volt az elektromos vezetés sávelmélete (1928, Bloch), a
legegyszerűbb modell, ami megmagyarázza, hogy egyes kristályok miért
szigetelők, míg mások miért jó vezetők. Itt az elektronok közötti
kölcsönhatást elhanyagoljuk, így egy bonyolult kvantummechanikai
soktestprobléma helyett csupán egyetlen elektronnak egy az
atomtörzsekből jövő periodikus potenciálban való mozgását kell egy
egyrészecskés Hamilton-operátorral leírnunk. Az elmélet szépen
reprodukálja egy minta tömbi részében lezajló jelenségeket.
A kvantumos Hall-effektus
felfedezése (1982) után fordult a fizikusok érdeklődése az elektromosan
szigetelő minták felületén megjelenő tökéletesen vezető "élállapotok"
felé. Ezek létezése, ill. számuk, a tömbi rész sávelméleti leírásában
megjelenő topologikus invariánsokkal adható meg, ez a tömb-él
korrespondancia. Ezen effektusok szisztematikus felderítésének
eredménye a "topologikus szigetelők periodusos rendszere" (Kitaev,
2009).
Az előadásban a
legegyszerűbb topologikus szigetelőről lesz szó, egy egydimenziós
kvantumdrótról, ami alrácsszimmetriával (királis szimmetria) bír.
Konkrét példa a poliacetilén Su-Schrieffer-Heeger modellje. Itt a tömbi
topologikus invariáns az alrács-polarizációnak feleltethető meg, az
élállapotok pedig a drót végein, az egyik alrácson található 0 energiás
kötött állapotok. Megmutatom, mi a szemléletes kapcsolat a tömbi
invariáns és az élállapotok között. Végül megmutatom, hogyan
általánosítottuk ezt az elméletet a periodikusan gerjesztett esetre.
Szemben a naív elvárással, a tömbi invariánsok ebben az esetben nem
kaphatók meg egy effektív (Floquet-)Hamilton-operátorból: az
invariánsok értékei függnek a gerjesztés részleteitől.
2014. október 2. (csütörtök) 13:00
Előadó: Vrana
Péter (BME, Geometria Tanszék)
Cím: Kvantum marginális probléma és összefonódási politópok
Kivonat |
Előadás
Egy többrészű rendszer
tiszta állapotának redukált sűrűségmátrixai (marginálisai) lehetnek
kevertek, így felmerül a kérdés, hogy az egyes marginálisok spektruma
tetszőleges-e, vagy együtt valamilyen feltételek vonatkoznak rájuk – ez
a kvantum marginális probléma. Ha kikötjük, hogy a rendszer állapota
egy rögzített összefonódási osztályban legyen, az további
megszorításokat adhat a lehetséges spektrumokra. Az előadásban arról
lesz szó, hogy milyen jellegűek ezek a megszorítások és hogyan lehet
(bizonyos esetekben) meghatározni azokat.
2014. szeptember 25. (csütörtök) 13:00
Előadó: Gergely
Árpád László (SZTE, Kísérleti és Elméleti Fizikai Tanszékek)
Cím: Tachion kozmológia, gravitációs lencsézés, fekete lyuk
kettősök gravitációs sugárzása és a fekete lyuk spinjének első
kimutatása a jet-ből
Kivonat
A fizika egyik
leghangsúlyosabb paradigmája az Univerzum 70%-át kitevő sötét energia.
Az kozmológiai állandó egyszerűsítő feltevése ellentmondásokhoz vezet.
Előadásom első részében egy dinamikai sötét energia modellt vázolok
fel, mely az összes mérvadó megfigyelési tesztet teljesíti.
Előadásom második részében a fekete lyukakra összpontosítok. Az
Univerzum legrejtélyesebb objektumai közé sorolható “égitestekről” ma
már tudjuk, hogy minden galaxis központjában megtalálhatók. Bár
definíció szerint láthatatlanok, jelenségek egész sora bizonyítja
létezésüket. Ezek közül a gravitációs lencsézést ismertetem
részletesebben. A galaxisok összeolvadása során a központi
szupermasszív fekete lyukak is egyesülnek, a jelenséget gravitációs
sugárzás kibocsátása kíséri. A gravitációs sugárzás közvetlen
kimutatása a közeljövőben várható, azonban a gravitációs sugárzáson
alapuló csillagászat egyik fő nehézsége a paraméterek közötti komoly
degeneráció lesz. Ezt elektromágneses kísérőjelenségek megfigyelésével
lehet feloldani. Ilyen megfigyeléseket szolgáltat többek között a
rádiócsillagászat, az ún. X-alakú rádiógalaxisok jelentős része
egymásbaolvadó fekete lyuk kettősökkel modellezhető. Végül röviden
ismertetem egy kiválasztott jet adatainak elemzését, melyből elsőként
mutattuk ki a jetalapnál elhelyezkedő fekete lyukspinjét.
2014. szeptember 18. (csütörtök) 13:00
Előadó: Varró
Sándor (Wigner FK, SZFI)
Cím: Haar Alfréd fizikai matematikája. I-II.
Kivonat |
Előadás
Haar Alfréd (1885–1933) a
múlt század első felében – Riesz Frigyes mellett – a matematika
legjelentősebb, nemzetközi hírű magyarországi képviselője volt.
Harmincöt publikációjában [1] megjelent számos eredménye az elméleti
fizikában is fontos szerepet játszik. Erre példaként említhetők a
Sturm–Liouville-féle differenciálegyenletekhez kapcsolódó ortogonális
függvényrendszerekre vonatkozó tételei [2a-b-c], amelyek a
Schrödinger-féle hullámmechanika konkrét felhasználásának alapját
képezik.
Előadásunkban kiemeljük a
Haar-féle ortogonális függvényrendszert (Haar-wavelet,1909) [2], a
több-dimenziós variációszámításban elért eredményeket (Haar-lemma,1922)
[3], valamint az invariáns mérték megkonstruálását lokálisan kompakt
topológikus csoportokon (Haar-mérték, 1932) [4]. Ez utóbbi eredmény
döntő jelentőségű volt a Hilbert-féle ötödik probléma (1900)
megoldásában. Időközben a Haar-mérték az absztrakt harmonikus analízis
nélkülözhetetlen eszközévé vált [5], és alkalmazást nyert a
kvantumelméletben is [6]. Megemlítjük még, hogy Haar a lineáris
egyenlőtlenség-rendszerekre vonatkozó Farkas-féle tételt (1901)
általánosította inhomogén rendszerekre [7], s mint az ma már jól
ismert, Farkas Gyula idevágó eredményei a modern optimalizáláselmélet
kialakulásában alapvető szerepet játszottak [8]. Megkíséreljük e
korszakalkotó eredmények hatását és utóéletét érzékeltetni. Elsősorban
a Haar-wavelet korai történetével és továbbfejlesztéséseivel
foglalkozunk, amelyek az 1980-as évektől a jelanalízisben [9] és az
információfeldolgozásban (pl. JPEG tömörítés) fontos szerepet kaptak.
Riesz 1911-ben, Haar
1912-ben kifejezetten Farkas Gyula közbenjárására került a kolozsvári
egyetemre: „Ime Riesz Frigyes társunk már javában megkezdte itteni
működését nagy lelkesedéssel a math. szeminárium körül is. ... Tegnap
levelet kaptam Haartól. ... Egyébiránt Haar levele oly mély hazafias
érzelmeket árul el, hogy mostmár nem is tartok attól, hogy ha egyszer
haza kerül, elveszítjük a külföldnek. ...” [8]. Haar Alfrédnak a múlt
századi magyar oktatás és tudományos közélet érdekében kifejtett
tevékenysége is múlhatatlan jelentőségű. „Az első világháború után
Erdélynek Magyarországtól való elcsatolása következtében az addigi
kolozsvári egyetem tanárainak el kellett hagyniok e várost és előbb
átmenetileg Budapesten, majd 1920-tól Szegeden folytatták működésüket.
Haar Alfréd és Riesz Frigyes az új szegedi matematikai szemináriumot –
amelyet később Bolyai Intézetnek neveztek el – hamarosan nemzetközi
tekintélyű matematikai centrummá fejlesztették. … Egyetemi előadásainak
tárgyát Haar leginkább az algebra számelmélet, analitikus geometria,
mechanika, differenciálegyenletek, variációszámítás, folytonos
csoportok elmélete területeiről választotta. Elsőrangú egyetemi előadó
volt, előadásai világosságban, logikus felépítésben mintaszerűek
voltak. …” Haar Alfrédtől könyv nem jelent meg. Azonban több igen
gondosan megírt jegyzetet készített.... Noha ezek az egyetemi előadások
sok eredeti részletet tartalmaznak, s mint egyetemi tankönyvek ma is
beválnának, a jelen összegyűjtött munkák közé való felvételükről már
csak terjedelmük miatt sem lehetett szó.” (Szőkefalvi-Nagy Béla,
Bevezetés, Haar Alfréd rövid életrajza [1]). Előadásunkban e nem
publikált egyetemi jegyzetekből is mutatunk be (tudomásunk szerint a
szélesebb tudományos közönség számára mindezidáig ismeretlen)
szemelvényeket.
Irodalom
[1] Haar A, Összegyűjtött Munkái. Sajtó alá rendezte Szőkefalvi-Nagy
Béla (Akadémia Kiadó, Budapest, 1959).
[2a] Haar A, Zur Theorie der orthogonalen Funktionensyteme ( Inaugural
Dissertation zur Erlangung der Doktorwürde der hohen
philosophischen Fakultät der Georg-August-Universität zu Göttingen,
vorgelegt von Alfred Haar aus Budapest). 1909, 1-49.
[2b] Haar A, Zur Theorie der orthogonalen Funktionensyteme (Erste
Mitteilung). Mathematische Annalen 69,
331-371 (1910).
[2c] Haar A, Zweite Mitteilung; ibid. 71,
38-53 (1911)
[3a] Haar A, Über die Variation der Doppelintegrale. Journal
für reine und angewandte Math. 149, 1-18
(1919).
[3b] Haar A, Über eine Verallgemeinerung de Du Bois-Reymond’schen
Lemmas. Acta Sci. Mathematicarum Szeged 1,
33-38 (1922).
[3c] Haar A, Über das Plateausche Problem. Math. Ann.
97, 127-158 (1926)
[4a] Haar A, Székfoglaló értekezés a Magyar Tudományos Akadémián (1932.
Április 18): A folytonos csoportok elméletéről. Mathematikai
és Természettudományi Értesítő, Budapest 49,
287-307 (1932).
[4b] Haar A, Der Maßbegriff in der Theorie der Kontinuierlichen
Gruppen. Annals of Mathematics (2) 34,
147-169 (1933)
[5a] Hewitt E and Ross K A, Abstract Harmonic Analysis I
(Vol. I: Structure of Topological Groups, Integration Theory, Group
Representations) (Springer-Verlag, New York, Inc., 1963, 1979).
[5b] Hewitt E and Ross K A, Abstract Harmonic Analysis II
(Vol. II: Structure and Analysis for Compact Groups, Analysis on
Locally Compact Abelian Groups) (Springer-Verlag, Berlin, Heidelberg,
1970)
[6] Mackey G W, The significance of invariant measures for harmonic
analysis. Colloquia Mathematica Societatis János Bolyai, 49., Budapest,
Hungary, 1985. In Szabados J and Tandori K (editors), Alfréd
Haar Memorial Conference Vol. II. (North-Holland Publishing
Company, Amsterdam, 1987) pp. 551-608.
[7] Haar A, A lineáris egyenlőtlenségekről. Mathematikai és
Természettudományi Értesítő, Budapest 36,
279-296 (1918). Über lineare Ungleichungen. Acta Scientiarum
Mathematicarum Szeged 2, 1-14 (1924).
[8] Prékopa András, Farkas Gyula élete és munkásságának jelentősége az
optimalizálás elméletében. In Martinás Katalin (Szerk.), Farkas
Gyula élete és munkássága. (ELFT Termodinamikai Szakcsoport,
Budapest, 2003) pp 9-26.
[9] Chui Charles K (Editor), WAVELETS : A Tutorial in Theory
and Applications. (Academic Press, Inc., Boston, San Diego,
1992)
2014. május 8. (csütörtök) 13:00
Előadó: Roósz
Gergő (PhD hallgató, SZTE Fizika Doktori Iskola)
Cím: Lokális kvencs kritikus Ising-láncban
Kivonat |
arXiv:1402.1744 [cond-mat.stat-mech]
A másodrendű
fázisátalakulások vizsgálata során az egyik nagy előrelépést
jelentette, amikor sikerült találni egzaktul kezelhető modellt, amelyen
tanulmányozható ez az átalakulás. Az első ilyen modell a kétdimenziós
klasszikus (és a vele ekvivalens egydimenziós kvantumos) Ising-modell
volt. Ezen modellek azóta is kiterjedt vizsgálatok tárgyát képezik.
Áttekintjük alapvető tulajdonságaikat, és a lokális kvenccsel
(paraméterek hirtelen helyi változtatásával) kapcsolatos korábbi
eredményeket. Egy speciális lokális kvenccsel kapcsolatban ismertetem
saját eredményeinket.
2014. április 17. (csütörtök) 13:00
Előadó: Lévay
Péter (BME, Elméleti Fizika Tanszék)
Cím: Egyszerű összefonódott fermionikus rendszerek geometriája
Kivonat
Az utóbbi időben a
kvantumos összefonódottságot mint egy olyan új erőforrást tekintik
melynek segítségével javunkra fordíthatjuk a kvantumos világ
furcsaságait. Ahhoz, hogy ezt megtehessük osztályoznunk kell tudni
valamilyen szempontok alapján ennek az új erőforrásnak a különböző
típusait. Meglepő módon a megkülönböztethetetlen részrendszerekkel bíró
rendszerek összefonódottsági típusai a megkülönböztethetetlen elemekből
álló fermionikus rendszerek összefonódottsági típusaiba ágyazhatók.
Egyszerű rendszerekre ez az eljárás érdekes módon a matematikai fizika
bizonyos, több mint száz éves múltra visszatekintő, klasszikus
eredményeivel hozható kapcsolatba. Ezek az eredmények - a fizikában
ezidáig csak egzotikus alkalmazásokban megjelenő - kivételes
Lie-csoportok geometriájával is kapcsolatosak. Az előadáson
megkíséreljük ennek az érdekes kapcsolatnak a bemutatását.
2014. április 10. (csütörtök) 13:00
Előadó: Gábris
Aurél (Szegedi Tudományegyetem/Cseh Műszaki Egyetem)
Cím: Dinamikai lokalizáció a kvantumos bolyongásban
Kivonat
A kvantumos bolyongás mára
úgy vonult be a tudományos köztudatba, mint egy kísérletileg könnyen
megvalósítható, de mégis változatos, összetett jelenségeket produkáló
unitér időfejlődési modell. Az egyik ilyen jelenség a dinamikai
lokalizáció. Előadásomban áttekintem az eddig elért elméleti és
kísérleti eredményeket az egydimenziós kvantumos bolyongást illetően.
Ezt követően térek rá a kétdimenziós esetre vonatkozó elméleti
eredményeinkre, és egy lehetséges kísérleti megvalósításra.
2014. április 3. (csütörtök) 13:00
Előadó: Simon
Ruijsenaars (Department of Applied Mathematics, University of
Leeds)
Cím: Calogero-Moser systems: A crossroads in mathematics and
physics
Kivonat (angolul) | Előadás | Integrable Systems Survey
The Calogero-Moser systems
are integrable $N$-particle systems that are connected to a great many
subfields of pure and applied mathematics, and that also find
applications in various areas of physics. In this lecture we aim to
survey this class of systems and their manifold relations to other
subjects. As an illustration, we sketch the connection of the
relativistic Calogero-Moser systems to the solitons of the classical
and quantum versions of the sine-Gordon equation
$u_{tt}-u_{xx}=\sin(u)$.
2014. március 20. (csütörtök) 13:00
Előadó: Hagymási Imre (Wigner FK, SZFI)
Cím: Kritikus viselkedés kiterjesztett
periodikusAnderson-modellben
Kivonat
Cérium és urán tartalmú
vegyületekben gyakran találkozunk az elektronok tömegének anomális
megnövekedésével. Erre magyarázat lehet az, hogy az f elektronok a
Fermi-energia közelében keskeny sávot alkotnak. A legegyszerűbb modell,
ami képes leírni az f és vezetési elektronokból is kialakuló
állapotokat a periodikus Anderson-modell. Utóbbi időben kiderült, hogy
egyes vegyületekben fontos szerepe lehet a vezetési és f elektronok
közötti Coulomb-kölcsönhatásnak. Az előadásban először áttekintjük az
irodalmi eredményeket, majd a saját eredmények kerülnek bemutatásra,
ahol a vezetési és f elektronok közötti kölcsönhatás szerepét
vizsgáljuk átlagtérelmélettel és variációs módszerrel. Kiderül, hogy
ezen kölcsönhatás újfajta kritikus viselkedés megjelenését okozhatja.
2014. március 13. (csütörtök) 13:00
Előadó: Balog János (Wigner FK, RMI)
Cím: Relativisztikus pont-mechanika
Kivonat |
arXiv:1401.7606 [math-ph]
Előadás |
arXiv:1402.6990 [math-ph]
Rövid történeti áttekintés
és a Currie ‒ Jordan ‒ Sudarshan-féle "no-interaction" tétel
ismertetése után a lehetséges kiutakat tárgyaljuk: a
Currie ‒ Hill-egyenletet, ill. kanonikus konstrukciókat, melyek között
a legismertebbek a Ruijsenaars ‒ Schneider-féle modellek 1 + 1
dimenziós téridőben.
2014. március 6. (csütörtök) 13:00
Előadó: Keresztes Zoltán (SZTE, Elméleti Fizikai Tanszék)
Cím: Sötét Energia és Tachion Skalármező
Kivonat
Sötét energia modellek
célja magyarázatot adni a világegyetem késői gyorsuló tágulására. A
világegyetem tágulásának gyorsuló tendenciáját eredetileg az Ia típusú
szupernóva-megfigyelésekből származtatott luminozitás-vöröseltolódás
reláció alapján fedezték fel, azóta pedig további csillagászati
megfigyelések is alátámasztották azt (kozmikus mikrohullámú
háttérsugárzás anizotrópiáinak szögeloszlása, barion akusztikus
oszcillációk). Jelenlegi tudásunk szerint a világegyetemben található
anyag mintegy 26%-át nem világító (sötét) anyag, míg 70%-át sötét
energia alkotja. Az előadásban röviden kitérek a ΛCDM modellre, a
kozmológiai modellek szupernova adatokkal való tesztelésére, a kozmikus
mikrohullámú háttérsugárzásra, a kozmológiai konstans problémára és
bemutatok lehetséges sötét energia jelöltre egy skalármezőt. A tachion
skalármező esetén tárgyalom a sík Friedmann univerzum időfejlődését, a
szupernova adatokkal jól illeszkedő paraméterek esetén pedig az
univerzum lehetséges végállapotait. A modellben a trajektóriák egyes
típusai a jövő evolúciójuk során ún. puha téridő szingularitásba
fejlődnek, amelyek átjárhatósága szintén tárgyalásra kerül.
2014. február 20. (csütörtök) 13:00
Előadó: Kis Zsolt (Wigner FK, SZFI)
Cím: Fényimpulzusok terjedésének adiabatikus kontrollálása
Kivonat
Atomi rendszerek
kvantumállapotának adiabatikus kontrollálása negyed évszázada
elméletileg és kísérletileg is kutatott terület. Kiterjedt közeg esetén
az adiabatikus kontroll módszerekkel közvetlenül a közeg
szuszceptibilitása befolyásolható. Ez által a közegben terjedő
fényimpulzusok viselkedését szabályozni lehet. Az előadásomban
bemutatom a témához kapcsolódó alapvető jelenségeket és röviden saját
eredményeimet is.
Szemináriumok 2013-ban
2013. december 5. (csütörtök) 13:00
Előadó: Görbe Tamás Ferenc (PhD hallgató, SZTE Fizika Doktori
Iskola)
Cím: A BC(n) típusú trigonometrikus Sutherland-modell és
duálisa
Kivonat |
Előadás
Egy Liouville értelemben
integrálható hamiltoni sokrészecske rendszer Ruijsenaars-duálisa annak
szimplektomorf képe, amelyben a kiindulási rendszer hatásváltozóinak a
duális részecske-pozíció változóit feleltetjük meg, és viszont. Az
előadás célja a BC(n) típusú trigonometrikus
Sutherland-rendszer és Ruijsenaars-duálisának jelenleg is folyó
vizsgálatában eddig elért eredményeink bemutatása.
2013. november 28. (csütörtök) 14:00
Előadó: Pusztai Béla Gábor (SZTE, Bolyai Intézet)
Cím: A hiperbolikus BC(n) Sutherland és a racionális BC(n)
Ruijsenaars-Schneider-van Diejen modellek: Lax mátrixok, dualitás és
szóráselmélet
Kivonat | arXiv:1109.0446
[math-ph] | arXiv:1304.2462 [math-ph]
Az előadás során
áttekintjük a hiperbolikus BC(n) Sutherland és a
racionális BC(n) Ruijsenaars-Schneider-van Diejen
modellekkel kapcsolatos eredményeinket. A modellek között fennálló
hatás-szög dualitási reláció bemutatását követően a szóráselméletüket
is ismertetjük.
2013. október 17. (csütörtök) 13:00
Előadó: Szalay Szilárd (Wigner FK, SZFI)
Cím: Kvantumösszefonódás és parciális szeparabilitás
Kivonat |
arXiv:1302.4654 [quant-ph]
A kvantummechanika
matematikai leírásában természetes módon bukkannak fel az úgynevezett
összefont (másnéven szeparálhatatlan) állapotok [1,2]. Ezzel szemben az
ilyen állapotban lévő kvantumrendszerekben a részrendszereken mért
fizikai mennyiségek korrelációinak megértése komoly kihívást jelent.
Nevezetesen, ezek a korrelációk a részrendszerek közötti kvantumos
kölcsönhatásokból adódnak, és nem modellezhetőek klasszikusan, hanem a
természet alapvetően kvantumos viselkedésének megnyilvánulásai,amiről
például a Bell-egyenlőtlenségek sérülése tanúskodik. Két
kvantumrendszer összefonódásának leírása jól ismert, akkor is, ha ilyen
rendszerek statisztikus sokaságát tekintjük (kevert állapotok), noha
ekkor az állapot összefontságának eldöntése, illetve mennyiségi
jellemzése nem könnyű feladat. A részrendszerek számának növelésével
feltárul, hogy az összefonódás struktúrája sokkal gazdagabb, mint amit
két részrendszer esetén láthatunk, és ez kevert állapotokra az
eldöntést és a mennyiségi jellemzést még jobban megnehezíti. Az
előadáson bemutatott eredmények ezekkel a kérdésekkel kapcsolatosak
[4,3]. 1. Tiszta állapotban levő kvantumrendszerek esetén a
részrendszerek parciális szeparáltsága könnyen megadható, azonban
kevert állapotok esetén az összefonódás struktúrájának még ez a
legdurvább közelítése sem volt megértett. Az előadásban bemutatjuk a
kevert állapotok parciális szeparabilitási osztályozását több
részrendszer esetére, mely a lehető legrészletesebb olyan osztályozás,
ami csak a parciális szeparabilitási tulajdonságokat veszi figyelembe.
2. További eredmény, hogy megadunk egy olyan kritériumrendszert,
mellyel elvben megállapítható egy kvantumállapotról, hogy melyik
osztályba tartozik. 3. Ezt a kritériumrendszert felírjuk olyan
mennyiségek segítségével is, melyek valamilyen szempontból
mennyiségileg jellemzik az állapotban rejlő különböző típusú
összefonódásokat.
Irodalom:
[1] I. Bengtsson, K. Zyczkowski - Geometry of
quantum states: An introduction to quantum entanglement, Cambridge
University Press, 2006.
[2] K. Horodecki et. al. - Quantum entanglement, Rev. Mod. Phys. 81
(2009), 865 (arXiv:quant-ph/0702225).
[3] Sz. Szalay - Quantum entanglement in finite-dimensional Hilbert
spaces, arXiv:1302.4654 [quant-ph].
[4] Sz. Szalay, Z. Kökényesi - Partial separability revisited:
Necessary and sufficient criteria, Phys. Rev. A 86, 032341 (2012)
(arXiv:1206.6253 [quant-ph]).
2013. szeptember 12. (csütörtök) 13:00
Előadó: Kovács István (Wigner FK, SZFI)
Cím: Rendezetlenség hatása a kollektív viselkedésre
Kivonat
A csapdázott atomi
rendszerek, szilárdtestek, társadalmi és biológiai hálózatok, az
internet, a neurális és jelátviteli hálózatok csupán néhány aktívan
kutatott példa a gyakorlatban óriási jelentőségű soktestrendszerekre,
ahol a rendszer inhomogenitásai, rendezetlensége döntő jelentőségű
lehet. A szilárd testekben jelen lévő rácshibák, szennyezések éppúgy új
jelenségekhez vezetnek, mint az emberek vagy éppen idegsejtek
különbözősége a hálózatokon belül. A komplex hálózatokban nem csupán az
egyes elemek térnek el egymástól, hanem a kölcsönhatásaik is rendkívül
heterogének lehetnek. Napjaink egyik legérdekesebb kérdése a területen,
hogy a mikroszkopikus szintű rendezetlenség milyen hatással lehet az
egyes rendszerekben a makroszkopikus szintű, kollektív viselkedésre. A
kérdés jelentősége messze túlmutat a klasszikus fizika határain, a
pénzügyi tranzakciók hálózatán keresztül a bankrendszer stabilitásán
át, a fehérje-fehérje kölcsönhatási hálózatok gyógyszertervezésben
betöltött szerepén túl a számítógépes vírusok terjedésének megértéséig.
2013. május 16. (csütörtök) 10:00
Előadó: Varró Sándor (Wigner FK, SZFI)
Cím: Alagút-effektus és Wigner-idő tegnap és ma
Kivonat
Az előadásban az
alagút-effektus felfedezésének és kutatásának rövid történeti
áttekintését adjuk, Hund (1927), Gamow (1928), Gurney és Condon (1928),
Nordheim és Fowler (1928) munkáitól kezdve. Bemutatjuk az
elektromágneses hullámterjedésnél és a kvantumos szűrésjelenségeknél
fellépő fáziskésések és prekurzorok szerepét. Foglalkozunk a Klein-féle
paradoxonnal (1929) is, és kitérünk az ún. Eisenbud-Wigner-időre
(1948,1955) valamint a Büttiker-Landauer-féle (1982) áthaladási időre,
aktuális kísérleti eredmények (a fotoemissziónál 2010-ben észlelt
attoszekundumos időkésés) tükrében. Újabb vizsgálataink alapján, az
alagút-effektust a "kvantum fázistéren" definiált Wigner-függvény
felhasználásával is elemezzük.
2013. április 18. (csütörtök) 13:00
Előadó: Fülöp Tamás (Wigner FK, RMI)
Cím: Másodrendű mozgásegyenlet az elektromágneses sugárzási
visszahatásnál
Kivonat |
arXiv:1207.0428 [math-ph]
Abból a feltételezésből
kiindulva, hogy a sugárzási visszahatás harmadrendű
Abraham-Lorentz-Dirac-egyenletének megoldásai közül egy másodrendű
mozgásegyenlet választja ki a fizikailag reálisakat, három módszert
szeretnék ismertetni a másodrendű egyenlet megtalálására. Két
analitikusan végigszámolható esetben a három módszer ugyanarra az
eredményre vezet. Mindkét rendszernél a sugárzási visszahatás egyrészt
egy sebességgel arányos csillapítást indukál, másrészt csökkenti a
külső erő nagyságát (vagy másként fogalmazva: egy véges pozitív
tömegrenormálódást okoz).
2013. április 11. (csütörtök) 11:00
Előadó: Diósi Lajos (Wigner FK, RMI)
Cím: Stochasztikus Schrödinger egyenletek és a kvantumfizika
alapjai
Kivonat | Előadás
Max Born rájött és Neumann
János kőbe véste, hogy a kvantumelmélet jóslatai statisztikusak, a
jóslattal egyidejűleg a hullámfüggvény pillanatszerű kollapszust
szenved. Ennek az egylövetű kollapszusnak időbeli felbontására jöttek
létre a stochasztikus Schrödinger egyenletek, mára sokféle
alkalmazással. Van, aki futó és tervezett optikai, kvantumdotos, stb.
kísérleteket ír le velük, van, aki új fizikát lát bennük. A szeminárium
ebben a keretben, elemi lépésekben ismerteti a stochasztikus
Schrödinger egyenleteket, nem rejtve az előadó saját eredményeit és
benyomásait sem.
Szemináriumi naptár
A szegedi Elméleti Fizikai
Tanszék története
Előzmények, további olvasmányok
A Szegedi Tudományegyetem
története
A fizika Szegeden
[Az Intézeti honlapon]
Az alábbi történeti összefoglaló a 90 éves a szegedi
természettudományi képzés című egyetemi kiadványban
jelent meg 2011-ben.
Az Elméleti Fizikai Tanszék
Nyomtatóbarát változat
Az Elméleti Fizikai Tanszék első vezetője Ortvay Rudolf
(1885–1945) volt. Ortvay Rudolf Farkas Gyula
(1847–1930) tanítványa a kolozsvári egyetemen. Ortvay Rudolf élete
hosszú ideig összeforrt a Ferencz József Tudományegyetemmel. Egyetemi
tanulmányait Göttingenben fejezte be, ahol abban az időben elsősorban a
matematika volt felülmúlhatatlan: David Hilbert, Hermann Minkowski és
Felix Klein hatása végigkísérte Ortvayt egész pályáján. 1909-ben Tangl
Károly professzor meghívására Kolozsvárra ment asszisztensnek. A tanári
munka mellett a folyadékok dielektromos állandója nyomásfüggésével
foglalkozott. Ebből írta doktori disszertációját, de érdeklődése az
elméleti fizikához húzta. Ösztöndíjjal Zürichben Peter Debye mellett,
majd Münchenben Arnold Sommerfeld mellett dolgozott. 1915-ben
magántanári kinevezést kapott, és ugyanebben az évben a nyugdíjba
vonuló Farkas Gyula helyére nevezték ki nyilvános rendkívüli tanárnak a
Ferencz József Tudományegyetemen. Az egyetemmel ő is Pestre költözik.
1920 őszén nyilvános rendes tanár lesz, Szegeden az egyetem
megnyitásától, 1921-től látta el az Elméleti Fizikai Intézet vezetői
teendőit. Kezdetben nem adta fel budapesti lakását, ingázott a két
város között, de mind több szállal kötődött a szegedi egyetem életéhez.
Az 1923/24-es tanévben a Matematikai és Természettudományi Kar dékánja
lett. 1924 és 1927 között ő szerkesztette a szegedi Acta
természettudományi értekezéseit. Oktatói munkásságának legjelentősebb
fejezete Szegeden a Bevezetés az anyag korpuszkuláris
elméletébe című előadássorozata. (Érdekességként
megemlítjük, hogy ezt az előadást József Attila, az 1924/25-ös tanévben
az egyetem hallgatója is felvette az indexébe). Az előadások anyagát
könyv formában is megjelentette, sőt akadémiai székfoglalójául is ennek
a könyvnek az ismertetését választotta 1925-ben. Szegedi működése
1928-ban szakadt meg, amikor a budapesti Elméleti Fizikai Intézet
igazgatója lett, Fröhlich Izidor helyén. A munkát ott folytatta, ahol
abbahagyta Szegeden, de a budapesti egyetem helyzetéből következően
jóval több lehetőség birtokában tovább alapozta a korszerű magyar
elméleti fizikát.
Ortvay távozása után
átmenetileg a Kísérleti Fizikai Intézet akkori vezetője, Fröhlich
Pál (1889–1949) látta el az Elméleti Fizikai Tanszék
vezetői teendőit is, majd 1930-ban az akkorra már jelentős tudományos
sikereket elért fizikust, Bay Zoltánt
(1900–1992) hívta meg az egyetem. Bay Zoltán egyetemi tanulmányait
Budapesten végezte, majd doktorálását követően ösztöndíjasként négy
évet töltött Berlinben. Tudományos tevékenységét ez idő alatt a
Physikalisch- Technische Reichsanstaltban, valamint a berlini egyetem
Fizikai-Kémiai Intézetében fejtette ki. Az aktív nitrogénre vonatkozó
kutatásai során e gázban spektroszkópiai úton szabad nitrogénatomokat
mutatott ki. Vizsgálati eredményeit idézni kezdte a nemzetközi
szakirodalom. Eredményesek voltak a hidrogénmolekula folytonos
ultraibolya spektrumára vonatkozó vizsgálatai is. Ezen a területen
mutatkozott meg először Bay Zoltánnak az az adottsága, amely
pályafutása során mindvégig jellemezte: rendkívüli áttekintő
képességével meglátta a tisztán tudományos kutatás alkalmas
eredményeiben a felhasználás lehetőségét, és kiváló gyakorlati érzékkel
fejlesztette találmánnyá a technika szférájába átültetett gondolatot. A
tanszékvezetői székét elfoglaló fiatal professzor nem tagadta meg a
kísérleti fizika iránti elkötelezettségét, és a rendelkezésére álló
szerény lehetőségek között laboratóriumot rendezett be magának a
jelenlegi Kísérleti Fizikai Tanszék második emeletén. A témát és a
kísérleti technikát készen hozta Berlinből. Ottani utolsó vizsgálatai,
melyről már idehaza a Mathematikai és Physikai Lapokban számolt be,
ritkított gázokban létrehozott nagyintenzitású áramlökésekre
vonatkoztak. A Szegeden elvégzett vizsgálatok igazolták Bay még
Berlinben megfogalmazott sejtését: az intermittáló áramlökések által
kiváltott színkép jellegét a nagy áramintenzitások határozzák meg. Az
eredményen túlmenően a kifejlesztett kísérleti technika értékes
segédeszközül szolgált azoknak a kutatóknak, akik az ívkisülésben
lejátszódó egyéb jelenségek vizsgálatával foglalkoztak. Az eszköz
alkalmas volt ugyanis olyan nagy áramerősségek rövid időtartamú
előállítására, amelyeket folyamatos üzemben, laboratóriumi méretű
kisülési cső nem viselne el. 1934 júniusában Bay megírt egy teljesen
elméleti fizikai tárgyú cikket, amelyben kis elmozdulások mechanikai
úton való felnagyításával foglalkozott. Nagyítóeszközül
csuklónégyszöget választva, megvizsgálta a rendszer kinetikáját,
valamint az elérhető szögnagyítás mértékét. A dolgozat klasszikus
mechanikai probléma kifejtésének tűnt, a gyakorlati alkalmazás
legcsekélyebb lehetősége nélkül. Ugyanez év végén azonban megjelent az
Orvosi Hetilap 50. számában egy cikk Bay Zoltán tollából, Egy
új rendszerű elektrokardiográphról címmel. A dolog előzménye
az, hogy Purjesz Béla és Rusznyák István belgyógyászokkal beszélgetve
azokat a fogyatékosságokat feszegették, melyek a korábbi, a
szíváramokat erősítés nélkül kijelző EKG-k használhatóságát
korlátozzák. A két orvosprofesszor ösztönzésére és tanácsai alapján egy
olyan elektrokardiográfot szerkeszt, amely felhasználja a rádiócsöves
erősítőtechnikát. Bay Szegeden kezdte művelni azt a kutatási területet,
amelynek problémaköre hosszú évtizedekre lekötötte érdeklődését. A
témaválasztás nem előzmények nélküli. Berlinben került kapcsolatba
Walther Wilhelm Bothéval (1891–1957), aki 1925-ben végezte el –
Geigerrel együtt – a Compton-effektusra vonatkozó klasszikus
kísérletét. Bay a sugárzás szórásának általánosabb problematikáját
kezdte vizsgálni a saját építésű Geiger-Müller-számlálókkal. A
nagyteljesítményű eszköz tényleges megépítésére azonban már Bay új
munkahelyének laboratóriumában került sor. 1936-ban ugyanis elfogadta
az egyeteminél lényegesen kedvezőbb kutatási lehetőségeket kínáló
Egyesült Izzó ajánlatát, ahol megbízást kapott a gyártelep
kutatólaboratóriumának vezetésére.
Bay Zoltán után
átmenetileg újra Fröhlich Pál lett a tanszékvezető, majd az 1939–40-es
tanévben őt Gombás Pál (1909–1971)
követte, aki 1941-ben az egyetemvisszahelyezéssel Kolozsvárra került.
Széll
Kálmán (1884–1952) – 1940-től haláláig vezette az
Elméleti Fizikai Tanszéket – tudományos pályáját a hazai és külföldi
egyetemeken folytatott tanulmányainak befejezése után, 1910-ben kezdte
meg azoknak a részletes vizsgálatoknak a közzétételével, amelyeket a
termoelektromos jelenségek termodinamikai kapcsolatainak felderítése
terén végzett. Kutatómunkáját ezután két és fél évtizedes gimnáziumi
tanári tevékenysége közben is rendszeresen folytatta. Főleg a
statisztikai mechanika diszciplínája kötötte le érdeklődését, s számos
figyelemre méltó eredményt tartalmazó dolgozata jelent meg hazai és
külföldi folyóiratokban a gázok és a sugárzás energiaingadozásairól,
valamint a két- és többatomos gázok rotációs és rezgési entrópiájáról.
Miután 1936-ban egyetemi szakelőadóvá, majd egyetemi tanárrá nevezték
ki, elsőrendű feladatának tartotta az elméleti fizika csaknem egész
területét felölelő előadásainak gondos kidolgozását. A nagy
felelősséget és elfoglaltságot jelentő egyetemi oktatással párhuzamosan
végezte tudományos kutatásait; nevezetesen, több tanulmányban
foglalkozott a gázoknak az újabb kvantumstatisztika szerinti
viselkedésével, tragikus halála előtt pedig a kritikus ingadozások
elméletéről szóló munkájának befejezésén dolgozott. Nemcsak mint
tudományos kutató, mint a statisztikai fizika elismerten kiváló
művelője, és nemcsak mint a tudomány fejlődésével az előadásaiban is
lépést tartó, hallgatóit mindenben segítő és támogató professzor
szerzett magának nagy érdemeket, hanem mint a tudomány eredményeinek
lelkes ismertetője, szélesebb körökhöz szóló közvetítője is.
Széll Kálmán halála
után, 1952-ben Horváth János (1922–1970)
a debreceni egyetemről került a szegedi Elméleti Fizikai Tanszék élére.
Szegedre hívásában döntő szerepe volt Budó Ágostonnak és egykori
tanárának, Szőkefalvi-Nagy Béla professzornak. Horváth János 1944-ben
Szegeden szerzett matematika-fizika szakos tanári diplomát, 1942 és 45
között díjas gyakornoka, 1944 novemberétől 1945 februárjáig megbízott
vezetője volt a szegedi egyetem Elméleti Fizikai Tanszékének. Ezután
Gombás Pál ajánlásával a Műegyetem Kémiai Fizikai Tanszékén, majd
Szalay Sándor meghívására a debreceni egyetem Orvoskari Fizikai
Intézetében dolgozott. Az elméleti fizika nagyon különböző területein
tevékenykedett, és ért el jelentős tudományos eredményeket. Kezdetben a
kvantumkémiai és általában az atomfizikai többtest-probléma
vizsgálatába kapcsolódott be. 1948 óta a tanszéken működött ugyanis a
vegyész végzettségű Pauncz Rezső (1920–),
aki az országban elsőként vezette be a képzésbe a Kvantumkémia
tantárgyat. A Gombás Pál és iskolája által kifejlesztett módszereket
alkalmazták és fejlesztették tovább. Pauncz Rezső pályája meredeken
ívelt fel 1956 után, amikor is külföldre távozott. Horváth János
érdeklődése ezután a differenciálgeometrián alapuló fizikai
térelméletek felé fordult. Az 50-es években az elemi részek
rendszerezésének munkájába kapcsolódott be a nemlokális térelméletek
keretei között, később ebből önállóan továbblépve a
vonalelem-geometriák által adott matematikai lehetőségek fizikai
felhasználásával foglalkozott. Könyveit és jegyzeteit (közülük talán
legismertebbek a Termodinamika és statisztikai mechanika
és az Optika) sok évfolyam fizikus és tanárszakos
hallgatói használták. Tanítványai szerették és tisztelték, csodálták
nagy tudását, sokoldalúságát, szigorát. Előadásaiban a fizika színes,
élő világként bontakozott ki, nemcsak a fizika ismerete, hanem
szeretete is sugárzott róla. Élénk nemzetközi tudományos levelezést
folytatott. Sokrétű és eredményes tudománypolitikai és
tudományszervezői tevékenységet fejtett ki. Elévülhetetlen szerepet
játszott a fizikus szak 1966-os szegedi elindításában. Hosszú éveken át
tagja volt az Akadémia Fizikai Bizottságának. Életének 48 éve során
csaknem húsz évet dolgozott az Eötvös Loránd Fizikai Társulat Csongrád
Megyei Csoportjában, előbb elnökségi tagként, majd elnökként.
1970-ben, Horváth
János halála után Gilde Ferenc (1928–)
vette át a tanszék vezetését. Működése ideje alatt folytatódtak a nagy
hagyományokra visszatekintő kvantumkémiai kutatások (Berencz Ferenc,
Maráz Vilmos), majd a 70-es évek közepétől nagyobb hangsúlyt kaptak a
szilárdtestfizikában is alkalmazható módszerek, továbbá megkezdődött a
fémklaszterek elektronszerkezetének és az elektron-molekula rugalmas
ütközéseknek a tanulmányozása (Benedict Mihály, Gyémánt Iván, Papp
György, Varga Zsuzsanna). A 80-as évek elejétől egyre jelentősebbé vált
a sugárzásanyag kölcsönhatás vizsgálata (Benedict Mihály), és sikeres
kutatások folytak a fotoszintetizáló rendszerek
elektrontranszport-folyamatának tanulmányozása terén is (Vass Imre).
1983-ban a
kvantumkémia kiváló kutatóját, Kapuy Ede
(1928–1999) professzort hívták meg az Elméleti Fizikai Tanszék élére,
és ezzel ismét fellendült – a térbelileg kiterjedt rendszerek
vizsgálatán belül – olyan kvantumkémiai módszerek kidolgozása és
konkrét alkalmazása, amelyek az elektronkorrelációt is figyelembe
veszik. Jelentős eredmények születtek a lokális és nemlokális hatások
szétválasztása, továbbá egy nyílt héjú önkonzisztens módszer
kifejlesztése terén (Kapuy Ede, Bartha Ferenc, Bogár Ferenc). A 90-es
évek elején került a tanszékre – a Statisztikus fizika
tantárgy óraadójaként – Iglói Ferenc, a Központi Fizikai Kutatóintézet
tudományos tanácsadója. Kapuy professzor nyugdíjba vonulása után,
1993-ban a tanszékvezetői székben először Gyémánt Iván
(1944–), majd Benedict Mihály (1948–)
követték egy-egy félévre és Iglói Ferenc
(1952–) két félévre mint megbízott tanszékvezetők.
1995–2008 között, Gyémánt
Iván tanszékvezetése alatt sikeresen folytatódott a
kicserélődés, a korreláció és a polarizáció szerepének tanulmányozása a
sűrűségfunkcionál elméletben, a belső héj ionizációs energiák
kiszámításában, az elektron-molekula ütközésekben, valamint a
fémklaszterekben (Gyémánt Iván, Varga Zsuzsa), és fontos eredmények
születtek a félvezetők elektrontranszportjának elméletében (Papp
György). Emellett a tanszék kutatási témái sokrétűbbé váltak, amit
erősített az új rendszerű doktori (PhD) képzés elindulása is. Minden
évben egy vagy két új doktorandusz kapcsolódott be az itt folyó
oktatásba és kutatásba. A fokozat megszerzését követően közülük többen
a hazai és külföldi egyetemek, kutatóintézetek oktatói és/vagy kutatói
lettek. Iglói Ferenc és tanítványai kiemelkedő eredményeket értek el a
statisztikus fizikában, nevezetesen az inhomogén, rendezetlen
rendszerek vizsgálatában, a fázisátalakulások kritikus exponenseinek
analitikus és numerikus meghatározásában és a hálózatok statisztikus
elméletében. 1995-ben került a tanszékre Fehér László,
a matematikai fizika, azon belül az integrálható rendszerek és a
konform térelmélet nemzetközi hírű kutatója. Az ő révén korábbi
munkahelyével, a Bolyai Intézettel is szorosabbá vált a tanszék
kapcsolata, tanítványa, Pusztai Gábor jelenleg is az Analízis Tanszék
oktatója. Ez idő alatt formálódott ki Benedict Mihály vezetésével a
kvantumelmélet elvi kérdéseivel, a kvantumoptikával, a fény és atomi
rendszerek koherens kölcsönhatásával foglalkozó új kutatói generáció,
közülük Czirják Attila és Földi Péter jelenleg is a tanszék oktatói.
Jelentős kutatásokat végeztek a gravitáció elméletében
a 90-es évek közepétől a tanszékhez kötődő Gergely Árpád
László és tanítványai. Toró Tibor
(1931–2010), a temesvári egyetem professzora tizenöt évig a tanszék
vendégprofesszoraként tartott nagy érdeklődést keltő asztro-részecskefizikai,
valamint – a 20. század vezető fizikusairól – tudománytörténeti
előadásokat.
2008-tól 2012 végéig
Benedict Mihály vezette a
tanszéket, ahol az előző időszak sikeres témáinak folytatása mellett az
évtized közepétől kezdve néhány újabb területen is számottevő
visszhangot keltő munkák születtek. Ide tartoznak az ún. nanomágnesek
sugárzási tulajdonságaira vonatkozó kutatások, másrészt a félvezetőkben
mozgó elektronok spinjének kvantumos manipulálását célzó spintronika
területén elért és jelentős nemzetközi idézettséget hozó eredmények
(Benedict Mihály, Földi Péter, Kálmán Orsolya).
|
|





